Well, we are all searching for the ultimate Automatic Differentiation tool, but we would be silly to claim that we found it! Therefore, TAPENADE could mean "Tangent and Adjoint PENultimate Automatic Differentiation Engine".

Honestly, we arranged this acronym after we chose the name! We simply liked the name TAPENADE because it is a typical ingredient of our local cuisine. It is made with capers, olives, and anchovies, and it makes a perfect apéritif in summer, on small toasts with a glass of cold rosé wine. Just in case you couldn't find some in your local grocery, here is a recipe of Tapenade from a famous book of provençal cuisine.

Include instructions accepted by Tapenade parsers:

Tapenade returns a syntax error while parsing my source files, that contain "include" statements. However, if I inline these includes manually in the source files, Tapenade parses the resulting source fine. Why is that and what can I do ?

The syntax of include statements and files that is accepted by Tapenade is more restrictive than the one accepted by most compilers. For technical reasons, we had to require that include files contain only declaration statements, and that the include or #include statement itself is in the declaration section of a procedure or of a module.

In other words, Tapenade will reject include files that contain instructions, control, or even worse other procedure or module definitions. Tapenade will also reject files that contain include calls in the middle of instructions or control.

You must modify your source files accordingly.

Please notice that if you use the #include directive, you may consider running your source files through fpp or cpp first, and then feed Tapenade with the preprocessed source instead. In some favorable situations, Tapenade might even be able to re-install the #include calls back into the differentiated files.

Languages accepted by Tapenade parsers, Syntax Errors :

After calling for differentiation of my files, I get the
"Something went wrong during differentiation" web page, which tells me that there is a syntax error in my files. What can I do ?

Yes, this happens in many cases. First notice that there are many sorts of so-called "syntax errors", which result in slightly different error messages. You may get one or many of the following:

Syst: ff (No such file or directory)
Syst: Fortran Parser: ff No such file or directory: Interrupted analysis :
Some required file was not found. Typically an include file was not given.
Tool: Unknown suffix file ff
Tool: No parser for ff. File skipped :
TAPENADE tries to guess the language of the file from its suffix. Then it looks for a parser for this language. Either step may fail.
File: Fortran Parser: Lexical error at line nn in file ff, ... : There is some character or word at this line nn which is not understood in the current file's programming language (e.g. Fortran).
File: Fortran Parser: Syntax error at line nn in file ff :
At this line is some syntax construction which is not permitted by the current file's programming language (e.g. Fortran).
Syst: Unexpected source operator: op (xx): Interrupted analysis
Syst: Unexpected source list: ops (xx): Interrupted analysis :
This internal error says that one operator of the current file's programming language was forgotten in a preliminary stage of the tool. Please send us this error message so that we can fix it quickly.
Syst: Not a tree operator: text :
The parser has failed, and sent an incorrect tree to the differentiator. This is probably an internal error, because the normal message should be the well known "Syntax error" above.
File: The file does not contain a top procedure : strangely enough, this message may appear as a result from a syntax error. Syntactically correct files must declare subroutines or functions. If, for any reason, no routine can be found, differentiation cannot start.
File: Fortran Parser: Lexical error at line 1 in program.f, Unknown character 'm' in column 1 to 5 : If your program uses the free format style and the file's suffix is .f or .F, you must select fortran95 as input language with the -inputlanguage fortran95 option in order to parse it without syntax error.

First of all, make sure that there are no missing or empty files. Then check that each file's suffix corresponds to its actual language:

.f or .F for Fortran,
.f90, .F90, .f95, or .F95 for Fortran90 or Fortran95,
.c or .C for C

Otherwise this is a "real" syntax error.

Our Fortran parser accepts all of the Fortran77 standard, plus most of the usual constructor's extensions, present or past (vax, sun, gould, connexion-machine, cray). Beware of possible conflicts between the standard and the extensions! For example in the standard, white-spaces are not significant: if the text functional is found in the code, it is seen as the keyword function followed by the identifier al, probably leading to a syntax error ! Therefore you mustn't call one of your code identifiers functional or subroutines. We couldn't change this rule because some old programs did strip away white spaces! Check that your file really complies with the standard or the constructor's extension. If this is the case, Tapenade should parse it correctly. If it does not, there is probably a bug in our parser. Please send us a message so that we can fix it quickly.

Our Fortran95 parser accepts of course Fortran90, and also a commonly used subset of the OpenMP and HPF extensions. Be careful with comments delimitor in the free format style: comments must start with a "!".

The Fortran90 standard limits the length of a line to 132 characters, and our Fortran90 parser does the same. However, as several compilers accept longer lines, Tapenade has a command-line option to increase this length limit. For instance
-linelength 200
sets the length limit to 200 characters.

Our C parser accepts ANSI C plus a few common extensions, BUT it doesn't accept C++ input.

If you really think your program complies with these standards, and our parser rejects it, please send us a message so that we can fix our parser. Notice furthermore that our parser does not support the cpp directives. For instance, we cannot parse files containing #define or #ifdef directives. Please run your files through cpp before sending them to Tapenade.

If the error you get is an internal error, please send us a message so that we can fix it !

Syntax of directives that modify differentiation (`$AD ...`):

I get the following error when Tapenade parses my source:
"File: Fortran Parser: Lexical error at line nn in foo.f95, Unknown keyword : c$ad nocheckpoint"
More generally, what is the exact syntax of the directives that I can use in my source to alter its differentiation?

Tapenade understands a small number of directives that can be used to alter the differentiated result. These directives must be provided in the source code as single-line comments that begin with $AD. Since the syntax of comments changes with the language, the syntax of tapenade directives changes accordingly, e.g. for directive "nocheckpoint":

In Fortran 77 :
```
C $AD NOCHECKPOINT
```
The C must be in column zero. There can be any number of white space (or none) before the $. Case is insignificant.
In Fortran 90-95 :
```
! $AD NOCHECKPOINT
```
The ! can be in any column. There can be any number of white space (or none) before the $. Case is insignificant.
In "not really ANSI-" C :
```
// $AD NOCHECKPOINT
```
The first / can be in any column. There can be any number of white space (or none) before the $. Case is insignificant but we suggest you use upper case for a better visibility.
In C :
```
/* $AD NOCHECKPOINT */
```
The initial / can be in any column. There can be any number of white space (or none) before the $. Case is insignificant but we suggest you use upper case for a better visibility.

The correct location of a directive in the source depends on the actual directive. At the moment, the available Tapenade directives are:

$AD NOCHECKPOINT, described here
$AD II-LOOP, described here
$AD FP-LOOP, described here
$AD BINOMIAL-CKP, described here
$AD CHECKPOINT-START, described here
$AD CHECKPOINT-END, described here
$AD DO-NOT-DIFF, described here
$AD END-DO-NOT-DIFF, described here

Language accepted by the A.D. engine ; Limitations:

I can see that Tapenade differentiates Fortran77 programs. What about Fortran95 or C ? What about their various constructors' dialects ? Do you have plans for object-oriented languages ? Do you differentiate programs with pointers, with records, with modules?

We are talking here of actual differentiation, not parsing. About parsing, see the "Syntax" question. We tried to differentiate correctly the standard features of Fortran (77 and 95) and of C, plus most of the usual constructor's extensions, present or past (vax, sun, gould, connexion-machine, cray). As far as differentiation is concerned, most of these extensions have little effect anyway. Of course there are possible bugs and a few restrictions that will be lifted progressively. We do not differentiate pure C++ constructs (Tapenade doesn't even parse them!). In the following list, parts in black are what Tapenade should differentiate correctly, parts in red are what is not differentiated:

Fortran 95 free source form : our Fortran95 handles it. Be careful with comments delimitor in the free format style: comments must start with a "!"
modules, BLOCKDATA : accepted and differentiated.
overloading : accepted and differentiated.
keyword arguments and optional arguments : accepted and differentiated.
derived types, structured types : accepted and differentiated
SWITCH/CASE statements : accepted and differentiated
pointers : accepted, analyzed and differentiated except in some cases in reverse mode
dynamic allocation, malloc's, free's : accepted and differentiated in tangent mode. In reverse mode, there are some limitations (that we must document some day) e.g. corresponding allocations and frees must live in the same procedure. In any case, we believe these constructs should preferably be kept out of the computational kernel, which should contain the fragment to differentiate.
namelist : accepted and differentiated.
vector notation, WHERE and FORALL constructs, mask's, SUM's and FORALL's : accepted and differentiated.
argument passing call-by-value, call-by-value-result, call-by-reference : accepted and differentiated.
interleaving declarations and instructions, declarations with initializations : accepted and differentiated. The attached comments are approximatively re-placed at their correct positions.
C if-expressions, e.g. x = 1 + (y<0?-y:y); : parsed but incorrectly differentiated, especially in reverse mode.
array constructors e.g. A(:) = (/X(2)-X(1),Y(2)-Y(1)/) : arrayConstructor are parsed but incorrectly differentiated in reverse mode.

Specifically for the reverse mode: a program piece that will be checkpointed (e.g. a procedure call) must be reentrant. This means that there must be a way to call it twice, at the cost of some manipulations to restore the initial state. For instance a procedure that modifies an internal hidden variable or state (think of IO pointers in files, or private counter variables...) is not reentrant. In this case, you must either transform the program piece to make it reentrant, or tell Tapenade not to checkpoint it.

Differentiation of object-oriented languages is still not in our immediate goals, and neither are the templates of C++.

Black-box procedures, unknown external or intrinsic procedures:

Tapenade complains about unknown external or intrinsic procedures, how can I teach it about them ?
I need to define a new set of library files or modify the existing *Lib files.
What is the syntax in there and what does it mean?

If the program you want to differentiate contains calls to EXTERNALs, INTRINSICs, library, or other "Black-Box" routines, then you may need to provide TAPENADE with some information about these Black-Box routines. You may also have to do this if we forgot to add into the standard library files the information on some intrinsic subroutines that you actually use.

It can also happen that you have the source of a procedure, but you don't want to give it to TAPENADE, because TAPENADE would then differentiate it in its own standard manner, and you know how to differentiate it better by hand! So make it a Black-Box by just forgetting to provide its source.

Some intrinsic functions, such as MAX, are not well treated when they have an unusual number of argument. For instance, MAX(x, y+z, 0.0) will not be analyzed, nor differentiated corectly. The workaroud is either to replace this by two nested calls to MAX, or to treat the 3-arguments MAX as another Black-Box function.

So, for whatever reason, TAPENADE has no source for a subroutine or function (suppose it is called BBOX). This has some unfortunate consequences. First, during type-checking, TAPENADE cannot compare the number and types of the actual arguments to the number and types of the formal arguments of BBOX. Furthermore, it doesn't know which arguments will be read and/or overwritten. More specifically for AD, TAPENADE doesn't know how to propagate activity through BBOX, i.e. which outputs of BBOX depend in a differentiable manner on which inputs of BBOX. Last but not least, TAPENADE doesn't know the name of the differentiated version of BBOX, in the case where you have programmed it already.

Notice that, although all this information is missing, TAPENADE will often generate good enough code, thanks to a number of conservative assumptions:

The types and the number of arguments are deduced from the actual usages. If these usages don't match, there will be an error message.
By default, a black-box routine is supposed to communicate with the calling code only through the calling arguments: TAPENADE supposes that the black-box routine doesn't use arguments through COMMON's and other globals. Warning: this assumption is not conservative: if the black-box routine actually refers to a global and nothing is done to tell TAPENADE about that, TAPENADE may produce wrong code!
All actual arguments are supposed to be possibly read inside the black-box routine, except of course the returned result of a function.
All actual variable-reference arguments are supposed to be possibly overwritten inside the black-box routine if it is an external or an intrinsic procedure. If it is an intrinsic function, we suppose no argument is overwritten.
Any variable argument of a differentiable type is assumed to return an output value that depends (in a differentiable way) on the input value of every argument of a differentiable type.
The differentiated routine is supposed to have the same name and shape as what would have been created by TAPENADE, i.e. BBOX_D or BBOX_B.

If you want to override the assumptions above, allowing Tapenade to produce better code, you may provide some knowledge of the Black-Box routines that are used in the program. The *Lib (old *ADLib files are now obsolete) are one way to give it this knowledge. Another way is to write dummy routines.

Warning: past versions of Tapenade supported separate *ADLib library descriptions, that described exclusively AD-related information, and that were supposed to complement another *Lib description that contained no AD-specific info. This is now obsolete. If you use *ADLib descriptions (through the former -extAD option), please merge them into the corresponding non AD-specific info in the corresponding *Lib description file (see example below). Then only use the -ext option to point to the new, merged *Lib description file.

SPECIFYING BLACK-BOX ROUTINES IN *Lib FILES:

The "*Lib" files contain information about library, intrinsic, external routines or any other Black-Box routine. This will help Tapenade produce more efficient code. For instance, there is one such file "F77GeneralLib" already in you installation "lib/" directory. You may modify it. You may also create your own files such as "MyAppliGeneralLib", in any "MyDirectory", and then you will pass these file names to your tapenade command using the -ext option.

    tapenade -ext MyDirectory/MyAppliGeneralLib ...

Each entry is about one subroutine or function, and gives info about number, type, intent of arguments, and possibly info related to AD. For example you might type, for a subroutine named BBOX and for a function called FBBOX:

subroutine bbox:
  external:
  shape:(param 1,
         param 2,
         common /c1/[0,*[,
         common /c2/[0,16[,
         common /c2/[16,176[,
         param 3,
         param 4,
         param 5)
  type :(float(),
         float(),
         arrayType(float(),dimColons(dimColon(none(),none()))),
         modifiedTypeName(modifiers(ident double), float()),
         arrayType(modifiedTypeName(modifiers(ident double), float()),
                   dimColons(dimColon(none(),none()))),
         boolean(),
         arrayType(character(),dimColons(dimColon(none(),none()))),
         character())
  ReadNotWritten:     (1, 0, 0, 0, 0, 0, 1, 1)
  NotReadThenWritten: (0, 0, 1, 0, 0, 0, 0, 0)
  ReadThenWritten :   (0, 1, 0, 1, 1, 1, 0, 0)
  deps: (id,
         1, 1, 0, 0, 0, 0, 0, 0,
         1, 0, 0, 1, 0, 0, 0, 0,
         0, 0, 0, 0, 0, 0, 0, 0,
         0, 1, 0, 1, 1, 0, 0, 0,
         0, 0, 0, 0, 0, 0, 0, 0,
         id,
         id)

function fbbox:
  intrinsic:
  shape: (param 1, param 2, result)
  type: (float(), float(), modifiedTypeName(modifiers(ident double), float()))
  ReadNotWritten:    (1,1,0)
  NotReadThenWritten:(0,0,1)
  NotReadNotWritten: (0,1,0)
  derivative: binary(call(none(), ident fbbox, expressions(metavar X, metavar Y)),
                     mul(realCst 2.0, metavar X),
                     expressions(binary(metavar X, none(), add(intCst 5, metavar Y)),
                                 binary(metavar Y, none(), div(realCst 1.0, metavar Y))))

The "external:" line states that the procedure is external. For an intrinsic, just replace this line by "intrinsic:".
The "shape:" part is necessary, because it defines the (arbitrary) order in which arguments will be referred to in the sequel. Its syntax is either param N that designates the N-th formal parameter, or result for the returned value if BBOX is a function, or common /xx/[0,8[ for an argument which is found from offset 0 to offset 8 in common /xx/.
All next lines are optional. If they are missing, the corresponding conservative assumptions are made.
The "type:" part gives the types of each argument, in the same order. The syntax of a type is rather heavy: we didn't find the time to make it cleaner yet, sorry! Actually it's the internal tree representation of the type inside Tapenade memory. In BNF-like, a TYPE can be:


TYPE ::= none()
(unspecified type, mostly means you don't want to care about specifying it)

TYPE ::= float()
(the primitive floating point type (Fortran REAL's or C float's)

TYPE ::= complex()
(the primitive type of complex numbers)

TYPE ::= integer()
(the primitive type of integers)

TYPE ::= character()
(the primitive types of characters)

TYPE ::= boolean()
(the primitive type of booleans)

TYPE ::= modifiedTypeName(modifiers(MODIFIERS), TYPE)
(MODIFIERS being a list of mostly ident and intCst such as double or 16
 for primitive type size modifiers)

TYPE ::= arrayType(TYPE, dimColons(DIMS))
(for arrays with a fixed number of dimensions)

DIMS ::= DIM
DIMS ::= DIM , DIMS

DIM ::= dimColon(BOUND, BOUND)
BOUND ::= none()
(for an unspecified dimension lower or upper bound)
BOUND ::= intCst N

TYPE ::= arrayType(TYPE, dimColons())
(for arrays with any number of dimensions)

TYPE ::= pointerType(TYPE)
(for a pointer to another type)

TYPE ::= void()
(void type, e.g. the return type of a subroutine, or the type of "nothing".
Probably useless in the present context)

For example, real*8 is written
modifiedTypeName(modifiers(intCst 8), float())
Arrays are built with the combinator "arrayType", that binds the array elements' type with a list of dimensions ("dimColon") which are pairs of the lower and upper bound. So far, these bounds are not very useful, so you might just as well leave them as "none()" or even use the arrayType(TYPE, dimColons()) form. Take a look at F77GeneralLib to find more examples.
This mechanism is far from being complete. For example, there is still no syntax for structured argument types ("derived types"), although they are handled well inside Tapenade. Nothing exists for named arguments, nor for a variable number of arguments. For a variable number of argument, you may have to create a *Lib entry for each number of arguments that actually occurs in your code.

In addition to this, there is our "metavar" type:


TYPE ::= metavar NAME

This metavar type represents any type. If it appears with the same NAME several times in the list of types of the present procedure, each occurrence must match the same type. The value of NAME just indicates which "sort" of type should be there, i.e. if actual pattern-matching fails to find a solution type for the metavar, then TAPENADE will choose ident NAME. Otherwise you may name your metavar "foo" instead of "float", and it should work just the same. This mechanism is by no means complete, but it helps.
Look at function "SUM" in F77GeneralLib for a less trivial use of metavars: in SUM, the metavar lets you specify that it takes an array of REAL and returns a REAL, or takes an array of REAL*8 and returns a REAL*8, or even an array of INTEGER and returns an INTEGER.

The "ReadNotWritten, NotReadThenWritten, ReadThenWritten, NotReadNotWritten" info gives the read-write signature of each argument. There is 1 for one argument when there exists at least one execution case of the procedure for which at least a part of this argument is "affectedInThisWay", where "affectedInThisWay" is the name of the info (i.e. one of ReadNotWritten, NotReadThenWritten, ReadThenWritten, NotReadNotWritten). This is a new notation, valid from version 3.6 on. This new notation replaces the deprecated, previous notation (R, NR, W, NW) which had a different meaning, less accurate. Although the deprecated notation is still accepted, we advise you to switch rapidly to the new notation in your home-made libraries.

The "deps:" entry is related to AD. It is the differentiable dependency matrix, of each output value with respect to input values, for each argument. The matrix is square (id elements count for one row), and the order of the rows is the order of the parameters as listed in the "shape:" entry for this procedure. The same holds for the order of the columns. For example, the element in row 2, column 5 specifies whether the output value of param 2 depends on (i.e. "has a non trivial-zero derivative with respect to") the input value of the variable from offset 16 to 176 in common /c2/. Here there is a zero, meaning a trivial zero derivative, i.e. no dependency. For example here, the result in parameter 2 depends on the input parameters 1 and 2, the result in the first variable in common /c2/ doesn't depend on any input, and the result in the tail array of /c2/ depends on the inputs in parameter 2 and in the whole of /c2/. An "id" entry instead of a complete line states that the argument is left unmodified, which is a stronger information than a line with just one "1", because it implies that the partial derivative is certainly "1.0". This is the case here for parameters 1, 4, and 5. On the other hand, parameter 3 is overwritten, but of course depends on nobody, since it has a non-differentiable type. For the same reason, nobody depends on parameters 3, 4, and 5. Notice also that nobody depends on the input in /c1/: it is an output only.

The other thing you may want to specify is the actual derivative of the black-box procedure. Three main possibilities:

It may happen that after activity analysis, TAPENADE finds out that the differentiated program does not actually need to differentiate the black-box. In other words, no argument of the black-box is active. Then you're very lucky, there is nothing you need to do!
If the routine really has active arguments, then it may happen that it is actually a function, and a simple one so that you can define the partial derivatives of its output with respect to each input, as a simple cheap expression. This can include calls to another intrinsic. TAPENADE can use those partial derivatives both in tangent and reverse mode. Think for example of COS(X). There's only one partial derivative you need to specify which is the partial derivative of the result wrt the first (and only) argument, and this derivative is -SIN(X). To specify this, the "derivative:" entry in the "*GeneralLib" file gives a pattern that must match the original call, and patterns that defines each partial derivative. Here again, the syntax is ugly because we didn't find the time to clean it yet. Sorry again! Let's recall what we wrote for the function fbbox above:
```
function fbbox
  derivative: binary(call(none(), ident fbbox, expressions(metavar X, metavar Y)),
                     mul(realCst 2.0, metavar X),
                     expressions(binary(metavar X, none(), add(intCst 5, metavar Y)),
                                 binary(metavar Y, none(), div(realCst 1.0, metavar Y))))
```
The parts in green are completely meaningless, but must be respected because TAPENADE expects to find them there.
In this example, one can find, in order, the pattern that must match the actual call, therefore instantiating the metavariables X and Y, then an expression which is a common factor to all partial derivatives (which can be "none()" if there is no common factor), then the list of each partial derivative of the function's result with respect to each metavariable: for each metavariable key, there is an expression that defines the corresponding partial derivative expression, which has to be multiplied by the common factor if present. For instance in the above example, we have expressed that the partial derivative of FBBOX(X,Y) with respect to X is the expression 2.0*X(Y+5) and its partial derivative with respect to Y is the expression 2.0*X/Y. Notice that we didn't give a "deps:" entry, because the default for an intrinsic function is just what we want! More examples can be found in the F77GeneralLib file, for instance the specification of the partial derivatives of COS mentioned above.
If there is no way to define the partial derivatives explicitly, then you must write and provide the derivative code of the black-box routine for the current differentiation mode (e.g. tangent, adjoint,...). Follow the message issued by TAPENADE to know which inputs (resp. outputs) of the black-box must be considered active. Follow the syntax that TAPENADE has chosen when generating the calls to this differentiated black-box in the differentiated code. Then simply write these differentiated external routines by hand in a separate file, using your preferred method/algorithm. When everything else fails, you may even use divided differences, always at the cost of some accuracy. Finally link the resulting code with the rest at the end of compilation time.

Please notice that these *Lib files are not able to represent all you would like to. For example, there is no support for procedures with variable number of arguments or named arguments. We hope it can be useful in most situations, though, until we devise a better and more complete syntax for these *Lib files.

SPECIFYING BLACK-BOX ROUTINES WITH DUMMY ROUTINES:

Sometimes the *Lib files cannot express some behavior of the black-box procedure, Tapenade does not understand this information well and doesn't differentiate the black-box procedure correctly. Sometimes also, the syntax of the *Lib files is really painful and one looks for a simpler method. Here is a possible simpler method that you can use. Write a dummy definition of the problematic black-box procedure, just like a standard procedure, with statements that just "represent" the data dependences of the actual procedure. We mean that the computations inside the dummy procedure may be totally wrong and meaningless, provided they implement the same differentiable data-dependencies between the inputs and the outputs. In other words again, for each output z that depends in a differentiable way on inputs ,say, x and y, just write a statement like


z = x*y

in the dummy procedure. Give this dummy definition only to the differentiation process, and remove the differentiated dummy procedure from the differentiated code returned by Tapenade. Finally, write by hand the correct differentiated black-box procedure and link it with the differentiated code returned by Tapenade.

Other Differentiation Modes:

I need higher-order derivatives, Hessians, Taylor series.
I need the full Jacobian Matrix.

In its present form, Tapenade builds programs that compute directional derivatives and gradients, i.e. in our jargon the forward and the reverse mode of A.D. Tapenade does not provide Jacobians, nor higher-order derivatives, nor Hessians, nor Taylor series.

However, there are ways to cope with that. For example, one can use the forward mode twice, to get directional second derivatives. We know of some people who have tried that with Tapenade, and apparently it worked. Notice however that this is certainly less efficient than a specific mode for second derivatives. One reason for that is that if you use the forward mode twice, you get two redundant copies of each computation of the first derivatives!

Then, from the higher-order directional derivatives, you can derive the higher-order Hessian tensors. This is sometimes more clever than computing these tensors from scratch, because one may take advantage of the tensor's symmetries. This question is discussed for example in GriewankUtkeWalther97

Tapenade does nothing about Taylor series nor intervals. These two could be interesting new modes to include into Tapenade, but this is not in our current plans.

Many applications need the Jacobian matrix. Here are some ways to get it:

There could be a special purpose differentiation mode, propagating a partial Jacobian throughout the execution of the original program. This was implemented once into Odyssée, and the results were interesting, though slightly disappointing. This mode was not maintained in the next version of Odyssée (1.7). However there is a potential source of optimization coming from array analysis in regular loops, as explored in TadjoudineEyssetteFaure98
One can compute it column by column, by repeated executions of the forward mode, one execution for each direction in the origin space. i.e. for each element of the Cartesian basis of the input space. Actually fewer directions are required when the Jacobian matrix can be shown to be sparse enough (see the litterature, e.g. the Griewank-Walther 2008 book [GrieWalt08]). This can be improved by computing the derivatives for many directions in the same run. This is the so-called vector mode or multi-directional mode, first found in ADIFOR and available in Tapenade. Multi-directional mode can exhibit some parallelism, as shown in BuckerLangMeyBischof01. As compared to ADIFOR, Tapenade brings the novelty that differentiated instructions, which are now loops, are gathered using a special data-dependency analysis. This reduces the overhead due to the numerous one-instruction loops.
One can compute it line by line, by repeated executions of the reverse mode. Due to the intrinsic difficulties of the reverse mode, this is recommended only when the number of inputs is larger than the number of outputs, but on the other hand this can benefit from specific improvements of the reverse mode such as a better detection of common sub-expressions in derivatives.

Type mismatches:

Tapenade Type-Checker sends me a lot of messages of the form:
(TC16) Type mismatch in assignment: REAL*8 receives DOUBLE PRECISION
What do they mean? Are they important? What must I do?

These messages may be important, but in many cases they are only "paranoiac" warnings. Your compiler may perfectly well accept that an argument of kind DOUBLE PRECISION is passed to a procedure that expects a REAL*8 or vice-versa. However this is against the Fortran standard, and it may be the cause of portability problems in the future. This is why Tapenade complains while your compiler doesn't.

For instance g77 does not complain on:


real*8 var
var = 1.0d0

but Tapenade does because the standard says that 1.0d0 is DOUBLE PRECISION and not REAL*8.

More importantly concerning AD in the reverse mode, the PUSH and POP procedures -- that are used intensively -- rely on an exact knowledge of the size in bytes of their argument. So at the minimum you should check that the sizes of these types match on the machine/compiler you will use, and that these are the sizes that Tapenade will use. To check the sizes on your machine/compiler, refer to the beginning of the FAQ section on validation of the differentiated programs

. To modify the sizes used by Tapenade to adapt them to the results of the above check, use the command-line options -r8 etc.

Anyway, all these precision problems are a nigntmare. We agree that most of the messages that Tapenade sends about this are a nuisance. Most probably you can neglect them. Maybe some day we shall offer an option to hide them away.

Nevertheless it still occurs sometimes, especially with Fortran95, that these messages indicate bugs in Tapenade. For instance Tapenade may have lost a dimension of an array. In this case, it is unlikely that differentiation will work. In this situation, when you see that your program is obviously correct and Tapenade complains, please send us a message so that we can improve Tapenade.

Aliasing problems:

I get the following message from Tapenade:
(DF02) Potential aliasing in calling function Func, between arguments arguments
What does it mean and is it important?

This means that Tapenade detected a memory overlap between arguments of ranks n₁ and n₂ of a call to a subroutine or function.

What is aliasing? Suppose a subroutine has many arguments (i.e. formal parameters or commons or globals...) At each call site, each of these formal parameters is given an "actual parameter", i.e. a reference to an actual variable, scalar or array, or an expression, or a constant... Aliasing happens when the same actual parameter is given to two different formal parameters. and one of these two formal parameters is overwritten by the subroutine. More generally, it happens when two actual parameters overlap in memory, and at least one may be overwritten. Please notice that such aliasing results in code that does not conform to the Fortran standard. e.g. see MetcalfReid96 section 5.7.2 page 91. This is an important warning, because Tapenade, like most static analysis tools, analyses each subroutine in its own local context, i.e. assumes that each formal parameter is a different memory location. And this assumption leads to a generated program (differentiated) that will fail if there is aliasing. For example:


subroutine F(real a, real b) {
  a = 3*b
}

would be differentiated in the reverse mode as (grossly) :


subroutine F_B(real a, real ab, real b, real bb) {
  bb = bb + 3*ab
  ab = 0.0
}

and this works fine as long as the actual a and b are different variables. But if a=b=x, F does x = 3*x, and what you want for F_B is xb = 3*xb. If you check, this not what you get by calling the above F_B. Similar problems arise in most program transformations, such as parallelization or partial evaluation, or others...

Notice however that aliasing, here detected by a static analysis, is by essence undecidable. Therefore Tapenade may detect aliasing when there is none! Also, it is frequent that, although there is aliasing, the differentiated program will run fine. It is the responsibility of the end-user, who knows the program, to check that his aliasing is harmless. Usually, when aliasing is really a problem, one can easily fix that by introducing temporary variables, so that memory locations of the parameters do not overlap.

Missing differentiated routines for intrinsic or Black-Box routines:

I can't compile my code because it misses the differentiated routines for some intrinsics, externals, or Black-Box routines.
I get a compiler message saying it needs to link with DCMPLX_B
How do I define the adjoint of an intrinsic routine?

This is perfectly natural.

In your original code were Black-Box routines, such a DCMPLX, i.e. either INTRINSICs or EXTERNALs or other routines for which you didn't provide the source. As a consequence, Tapenade has placed in the differentiated code a call to the differentiated routine DCMPLX_D in tangent mode or DCMPLX_B in adjoint mode, and sent you a message requesting you to define these new routines. Now is the time to do it.

Take the example of DCMPLX with 2 arguments:


    cc = DCMPLX(rr,ii)

This call builds a DOUBLE COMPLEX number with real part rr and imaginary part ii, and puts the result into variable cc.

The variables on which DCMPLX operates are rr, ii and cc. To consider only real numbers, let's split cc into its real and imaginary parts cc.r and cc.i. Since rr and ii may be used later, we consider them also as (unchanged) outputs of DCMPLX. Similarly cc can be seen as an (unused) input. All in all, DCMPLX operates from R⁴ to R⁴, with some conventional ordering e.g.:


   (rr ii cc.r cc.i)

We can thus write the Jacobian matrix of DCMPLX, which is in this case simply:

as the output cc.r receives exacty rr, the output cc.i receives exacty ii, and neither rr nor ii are modified.

The tangent differentiation of DCMPLX just implements the matrix-times-vector product with this Jacobian, i.e.


   (rrd   )   (1 0 0 0)   (rrd   )
   (iid   )   (0 1 0 0)   (iid   )
   (ccd.r ) = (1 0 0 0) * (ccd.r )
   (ccd.i )   (0 1 0 0)   (ccd.i )

hence the definition of DCMPLX_D you must provide:


      function DCMPLX_D(rr, rrd, ii, iid, cc)
      DOUBLE PRECISION rr,rrd,ii,iid
      DOUBLE COMPLEX cc, DCMPLX_D
      DCMPLX_D = DCMPLX(rrd,iid)
      cc = DCMPLX(rr,ii)
      end

The adjoint differentiation of DCMPLX just implements the matrix-times-vector product with the transposed Jacobian, i.e.


   (rrb   )   (1 0 1 0)   (rrb   )
   (iib   )   (0 1 0 1)   (iib   )
   (ccb.r ) = (0 0 0 0) * (ccb.r )
   (ccb.i )   (0 0 0 0)   (ccb.i )

hence the definition of DCMPLX_B you must provide:


      subroutine DCMPLX_B(rr, rrb, ii, iib, ccb)
      IMPLICIT NONE
      DOUBLE PRECISION rr,rrb,ii,iib
      DOUBLE COMPLEX ccb
      rrb = rrb +  DBLE(ccb)
      iib = iib + DIMAG(ccb)
      ccb = DCMPLX(0.d0)
      end

The above equation is a "vectorial" assignment in R⁴, which is done "in parallel". Therefore we were careful not to reinitialize ccb before it is used to update rrb and iib. Also, since this is adjoint mode, it is no use to return the value of cc

ISIZE* constants all over the place:

The differentiated program doesn't compile because it contains undefined constants of the shape ISIZE*.
Tapenade sends messages "user help requested" about new constants it needs.
I don't want to define all these ISIZE* constants. I want Tapenade to use size() instead

Differentiated code can need the user to define constants, for instance about array size, because Tapenade cannot find them by static analysis of the source program. See the explanations about messages AD10 or messages AD11 and AD12.

In order to compile the differentiated program, you must create this DIFFSIZE file, in the form of an include file or of a module, depending of the application language. Details can be found here.

Messages "user help requested" are here just to remind you of that.

In some cases, you may tell Tapenade to place run-time calls to size() rather than using these constants. This is possible in recent Fortran77 and in Fortran90. Use command-line option "-noisize" to do so in Fortran90, "-noisize77" in Fortran77. There are rare situations where this doesn't work, though, in which case you may still have to provide a few ISIZE* constants.

Divisions by Zero and NaN's:

The differentiated program returns NaN's in the derivative variables. However my original program is clean and doesn't return NaN's !

Differentiation can introduce NaN's in the resulting program, because programs are sometimes non differentiable. (You may take a look at the FAQ item about the domain of validity of derivatives) In general, AD is in trouble when it comes to differentiating a function at places where it is not differentiable.

In this situation, we prefer that the differentiated program return NaN, which at least shows that something went wrong. This is probably better than silently returning a wrong derivative that may lead to other wrong results later. The end-used can then analyse the original program, and maybe transform it to make it differentiable.

However there are situations where Tapenade can do a slightly better job, automatically. Non-differentiablility often occurs for SQRT, LOG, and exponentiations. For SQRT, we can do something a little more clever than returning NaN, but only in one particular case:
Suppose instruction is


    a = SQRT(b)

the tangent derivative instruction is


    ad = bd/(2.0*SQRT(b))

that returns NaN if b is 0.0. But if bd is also 0.0 at this time, then we feel it is safe to return


    ad = 0.0

On the other hand, we think it is not safe to test on b or a being 0.0 or close to 0.0. The reason is that in this case the derivative is really undefined, so it's up to the user to do something about it. It would be dangerous to return ad = 0.0 automatically. Only the user can do it by hand, and check that it "works" for the current application.

Something similar is done for exponentiations. Nothing is done for LOG. We should probably do the same as for SQRT!

A similar reasoning applies to the reverse mode: Tapenade generates statements that detect special cases and build 0.0 derivatives.

However there is a weakness in Tapenade when it comes to returning Nan's: unlike what happens in Adifor, there is no warning message printed at the moment when the Nan appears. Therefore, in the very frequent case where the compiled code does not stop when the Nan appears, computation goes on as usual and it is very difficult to find the place where the problem originated. We are aware of this problem and this should be improved.

NaN's can also appear for a slightly different reason: for some given inputs, some functions have an output which is large, but not yet in overflow, whereas the derivative is definitely in overflow. Think of 1/x, whose derivative is -1/x**2. Again this requires a special treatment. One way could be to switch to double precision.

We recently ran into a very annoying NaN problem related to uninitialized variables. Please avoid using uninitialized variables in your code! Tapenade tries to send messages about uninitialized variables, but this is a typical undecidable question, so we cannot find all of them. The following summarizes the problem that we found on a very large code...


      subroutine TOP(x,y)
      real x,y
      real BAD(2)
      call SUB(BAD,x)
      y = BAD(1)
      end

      subroutine SUB(BAD,x)
      real x, BAD(2)
      BAD(1) = x*x
      BAD(2) = BAD(2)*x
      end

You can see that array BAD is not initialized. BAD(2) may very well contain something bad like a NaN. However this has no visible impact on this original code because the resulting x and y are not polluted by the NaN. Still this code is going to silently compute on NaN's, and you don't want this.
Now if we differentiate this code in reverse mode, the following statement appears in SUB_B:


      xb = xb + bad(2)*badb(2)

and if the initial BAD(2) is a dirty NaN, then this computes NaN times 0.0, which on some compilers evaluates to NaN, and the resulting xb gets corrupted!

Domain of validity of derivatives:

What does AD compute when the fonction is non-differentiable?
Why is the Tapenade derivative always 0.0 for my dichotomy-based resolution program?
To what extent can I trust the derivatives computed by Tapenade?
Is there a discontinuity in my function close to the current input?
How can I evaluate the differentiability domain around my current input?
Is there any support in Tapenade for non-differentiable functions?

If the Tapenade-differentiated code is executed right on a non-differentiable input, it may happen that the differentiated program returns NaN's as derivatives. See the FAQ item about divisions by Zero and NaN's.

Also, although it is hard to admit :-), there may be bugs in Tapenade :-( Therefore, you probably need to go through the validation process to make sure that the derivatives are correct, compared to Divided Differences. Although inaccurate and expensive, Divided Differences are robust and therefore return good enough derivatives for validation.

However, it may happen that the differentiated program just does not notice that it is on (or close to) a discontinuity. This is not a bug of Tapenade; this comes from the nature of AD. Think of a dichotomy-based program that solves f(x,y)=0, returning y as a function of x. The derivative of y with respect to x is in general nontrivial. Robust Divided Differences will actually return (an approximation of) the correct derivative. But AD will return 0.0, and this can be explained:
the dichotomy-based program actually sees f as a piecewise constant function, where each piece is of the size of machine precision. In other words, for values of x that differ only very slightly, the value of y is exactly the same, and thus the derivative is rightly 0.0. Only this is not what you had in mind when you wrote the program!

Apart from the immediate rule of thumb which is "don't even think of differentiating dichotomy-based code, don't even write it!", the conclusion is that programming often introduces discontinuities into perfectly differentiable mathematical functions, and AD can't do much about it (true, Divided Differences behave better on this question!). When this happens, the derivatives computed by AD are just useless or plainly wrong. All we can do is warn the user when this happens, which is when there is a non-differentiability "close" to the current point, i.e. around the current input values.

In Tapenade, there is an experimental differentiation mode that evaluates the domain of differentiabillity around the current point, following a given direction in the input domain. The command-line argument -directValid builds a special differentiated program which, given a point in the input space and a direction in the input space (very much like in the tangent mode), evaluates the interval of differentiability along this direction. This uses subroutines called VALIDITY_DOMAIN_...(,), which are defined in the file validityTest.f provided in the AD First-Aid kit. After execution of the differentiated program, the interval of differentiability around the given input point and following the given direction is found in
COMMON /validity_test_common/ gmin, gmax, infmin, infmax
where gmin (resp. gmax) is the lower (resp. upper) bound, and if there is no constraint on the lower (resp. upper) bound, then infmin (resp. infmax) is .TRUE.

Caution: If, inside the same execution, you need to perform several independent calls to the "directional validity" differentiated code, for different inputs or for different directions, then don't forget to reset the validity interval to ]-infinity,+infinity[ between two successive calls. Do this by resetting both infmin and infmax to .TRUE.

Using this mode in every direction of the Cartesian basis of the input space will give a box inside which derivatives and derivatives-based optimization are valid.

Differences with Odyssée :

I have been using Odyssée in the past. What are the modifications from Odyssée to Tapenade ?

Details on this question in the history of successive versions.

TAPENADE is the successor of Odyssée. Therefore, TAPENADE is an incremental improvement to Odyssée. However, we had to radically modify the internal structures of Odyssée to take profit of compilation theory and technology. The internal representation of a program is now a Call Graph, with one node per subroutine, and each subroutine is now a Flow Graph, whose nodes are Basic Blocks. Each Basic Block is equipped with a Symbol Table, and Symbol Tables are nested to capture scoping. Basic Blocks contain instructions, represented as Abstract Syntax Trees. Static analyses now run on this structure, and this yields an enormous speedup in differentiation time, with respect to Odyssée. Right from the beginning, this internal representation of programs was designed independently from a particular imperative language, like Fortran or C. For example data structures are already managed. In principle, adaption to C, say, just requires a C front-end and back-end, i.e. a C parser and a C pretty-printer.

About the differentiation model, TAPENADE is very similar to Odyssée. It still provides you with the forward and reverse mode of A.D. There are some improvements though:

The activity analysis, a static analysis that finds the variables that need not be differentiated, is now bi-directional. It detects the variables that do not depend on the independents, and the variables that do not influence on the dependents. This leads to fewer differentiated variables.
We included the TBR analysis, a static analysis for the reverse mode. It finds variables which, although they are overwritten during the forward sweep, need not be saved because they will not be used during the reverse sweep.
We implemented a new storage strategy for the reverse mode, named the global trajectory. This stores intermediate values on an external stack rather than on static arrays that thad to be dimensioned by hand by the user of Odyssée
Snapshots in the reverse mode are smaller, because they use In-Out analysis to find out variables that are really necessary for duplicate execution of the checkpointed piece of code.
The inversion of the control, in the reverse mode, is done on the Flow Graph. This gives a better, more readable transformed source, that the compiler can compile better.
TAPENADE provides vector (i.e. multi-directional) modes, similar to the ADIFOR's vector mode. It computes derivatives in many directions simultaneously. Derivative loops are gathered using data-dependency analysis.
Data-Flow analysis is used to optimize the transformed source, at the level of each Basic Block.

We provide two ways of using Tapenade: either by connecting to the web server, or by downloading it to install it locally. There is a graphical user interface based on HTML, and a simple command-line interface.

Documentation, Archives of the Mailing list :

What is the available documentation on Automatic Differentiation in general and specifically on Tapenade ?
How can I take advantage of the experience from previous users of Tapenade ?

Here is a short introduction to "what is AD?"
The web site of the AD community www.autodiff.org contains the most comprehensive documentation on AD.
About Tapenade, apart from the tutorial here, you should start by looking at the Tapenade reference article and at the Tapenade users manual.
Another good starting point is our Documents page.
If you subscribe to the tapenade-users mailing list, you will have access to the archive of previous discussions at the address: https://sympa.inria.fr/sympa/arc/tapenade-users.

Unsubscribe from the Mailing list

How can I unsubscribe from the tapenade-users mailing list?

From the e-mail address with which you subscribed to tapenade-users, send a message to sympa_inria@inria.fr, with subject:
unsubscribe tapenade-users
and en empty message body.
Don't hesitate to tell us if this doesn't work.

Want to cite Tapenade? :

What is the reference paper on Tapenade that I might cite in my paper ?

That's very nice of you !
We suggest you cite the Tapenade reference article. This link contains the bibtex for the reference article and the pdf of its preprint.

PUSH/POP mechanism :

Where are the PUSH and POP routines defined?

We provide you with the source of these routines in file adStack.c (plus files adStack.h and adComplex.h). You may download them by clicking on the "Download PUSH/POP" button in the differentiation result page, or else

In some cases, the compiler may complain that some required PUSH/POP procedure for some unusual type is not in adStack.c, e.g. _pushinteger16. In this case edit adStack.c and either uncomment the required procedure it if it is there or create it as indicated (see inside file adStack.c).

Original statements and results disappearing from the Reverse code :

My original procedure computed an output Y whereas the reverse differentiated procedure does not return the correct value of Y.
Some statements that are present in the original code have simply disappeared from the reverse code (this may even result in empty loops or if branches).

By default, the reverse mode of Tapenade performs adjoint liveness analysis. This means that some statements from the original program, which were "live" i.e. which computed something needed by the rest of the program, are not live anymore in the reverse differentiated program. This often occurs around the end of a forward sweep, just before the backward sweep. The reason is: a priori the only result you expect from the reverse differentiated program is the derivatives. In particular the original result of the original program is not considered as a necessary result of the reverse differentiated program. Therefore statements that are needed only for this original result become dead code. More explanations and a small example are in the TAPENADE 2.1 user's guide, specifically on page 33-34. A command-line option can toggle this mechanism off, see "-nooptim adjointliveness" on page 38.

For users who want the reverse differentiated program to preserve the original outputs of the original program, we advise first to toggle adjoint liveness analysis off. However this is not enough, because the PUSH/POP mechanism will naturally destroy several of the program's original results. We advise that you modify the differentiated program by hand, saving the variables you want into temporary variables at the end of the forward sweep, and restoring these variables at the end of the backward sweep.

Basic and extremely useful code preparation before differentiation

I have a code I want to differentiate. How should I proceed?

Just "Differentiating a code" does not mean much, unless you know precisely which part of the code is the math function you want to differentiate, which are its "independent" inputs and "dependent" outputs, and maybe which differentiation mode you want to use. We advise you to follow the steps below. This way you will be forced to answer the above questions even before you start playing with Tapenade. These steps will also vastly ease your life when it comes to validate the differentiated programs. Finally, they will make our life easier if we are to help you, and if we have to debug Tapenade!

First thing is to decide which is the part of the code that defines the function you want to differentiate. It is certainly not your complete program! It must be a connex piece of code (call it the inside) with a unique beginning (call it the entry) and a unique end (call it the exit). This piece of code can very well contain calls to other procedures. Every run of your code that goes through the entry must then reach the exit. In particular, there must be no control jumps from outside to the inside, except to the entry. Similarly, there must be no control jumps from the inside to the outside, except from the exit. Make this "inside" piece of code a subroutine or function (in FORTRAN) or a procedure (in C). Your original code is therefore modified: you have created a new procedure, and now there is a call to this procedure in place of the original piece of code to differentiate. It now looks like (FORTRAN style):
```
          ... whatever code is before ... 
C Beginning of the function I want to differentiate
       CALL MYFUNC(x1, x2,..., y1, y2,...)
C End of the function I want to differentiate
          ... whatever code comes after ... 
```
It goes without saying, but make sure you use some mechanism to make necessary variables travel to and from the new procedure. You may use parameter passing, or FORTRAN common, or globals... as you wish. We shall call these variables the "parameters" of the procedure (even if they are indeed globals). It is very useful that you know these variables well, what they mean, what they are needed too, are they just used or just written and returned, or both, etc... Now you see why this preparation work must be done by someone who knows the code!
Apply Tapenade in the "no-differentiation" mode, which is command-line option "-p". This will trigger several analysis but will generate a source code that should be equivalent to the original code, without any differentiation. The interest is to check that Tapenade is able to parse your source files correctly. Another interest is to see the warning messages issued by Tapenade. Some of these messages may indicate situations where things can go wrong. Therefore, we advise you to type something along the lines of:
```
   $> tapenade -p -o nodifferentiated  "source files but no include files"
```
This will read all your source files (do not provide the include files in the command line because Tapenade will read them automatically when needed). Your source code will be parsed and analyzed, and this will result in a file nodifferentiated_p.msg. It contains a (verbous) list of all warning and error messages, that you should browse through, with the help of the documentation on messages. The explanations in the reference manual will help you find which messages can be discarded (e.g., very often, the implicit conversions between REAL*8 and DOUBLE PRECISION), and which ones can't. Tapenade should have generated by now a new source file nodifferentiated_p.[f/f90/c], that contains a duplicate of your original source.
Make sure this "non-differentiated" duplicate code produced by Tapenade compiles and runs. Check that its execution is equivalent to your original code's.

ALSO: CHECK THE SIZES OF PRIMITIVE TYPES:

If the program crashes, there is a small chance that this comes from the sizes of basic types on your system. To test these sizes, go into the ADFirstAidKit directory, then:

1) adapt the compilation commands $(FC) and $(CC) in the Makefile
2) make testMemSize
3) execute testMemSize
4) look at the sizes printed.

The standard Tapenade expects: integers:4 ; integers*8:8 ; reals:4 ; reals*8:8 ; doubles:8 ; complexes:8 ; complexes*8:8 ; complexes*16:16 ; double complexes:16 ; logicals:4 ; characters:1
if testMemSize on your system gives different sizes, use the type size options that change the default sizes to what your system expects.

THE FOLLOWING PREPARATION STEPS WERE USEFUL

FOR THE OLD VALIDATION METHOD ONLY

We keep them here for the record only, but they are not necessary!

Write a procedure that saves all these "parameters" of MYFUNC into some storage (can be static arrays), and a procedure that restores the saved values into these parameters. You may test them inside your modified code, just to make sure! Your code could now look like:


          ... whatever code is before ... 
       CALL SAVE_NECESSARY_PARAMS(x1, x2,..., y1, y2,...)
       CALL RESTORE_NECESSARY_PARAMS(x1, x2,..., y1, y2,...)
C Beginning of the function I want to differentiate
       CALL MYFUNC(x1, x2,..., y1, y2,...)
C End of the function I want to differentiate
          ... whatever code comes after ...

Call the new procedure twice in a row, inside the same execution. check you obtain the same results. So you will be sure that there is no unwanted side-effect or undefined-variable-used in your code to be differentiated. Your code could now look like:


       ... whatever code is before ... 
C Save what is necessary in the current state
       CALL SAVE_NECESSARY_PARAMS(x1, x2,..., y1, y2,...)
C Beginning of the function I want to differentiate
       CALL MYFUNC(x1, x2,..., y1, y2,...)
       res1_y1 = y1
       res1_y2 = y2
       ... 
C Prepare for the second run
       CALL RESTORE_NECESSARY_PARAMS(x1, x2,..., y1, y2,...)
C Call MYFUNC again
       CALL MYFUNC(x1, x2,..., y1, y2,...)
       res2_y1 = y1
       res2_y2 = y2
       ... 
       make sure all res1_yyy == res2_yyy 
C End of the function I want to differentiate
       ... whatever code comes after ...

Now choose which ones among the above "parameters" you want to differentiate (the "dependents"), with respect to which ones (the "independents"). Beware these must all be elements of the set of "parameters". We do not differentiate a procedure with respect to its local variables, constants, or with respect to variables that the procedure does not see. In particular, it happens that some of these parameters are dynamically allocated (resp. freed). Then it is essential that the allocation (resp. free) is outside of the procedure to be differentiated. On this question, see this note on an apparently inconsistent behavior between differentiated scalars and arrays. Although this is not as essential, it is also good politics to avoid dynamic allocation/freeing anywhere inside the procedures to be differentiated. This may cause hard problems especially with the reverse mode.

Why not try and compute a (approached) derivative by divided differences then? It's maybe a little early but you will need to do it anyway for the old validation step. Define a differentiated variable for each of the dependent and independent. Initialize them all to 1.0. Modify each independent inputs by "epsilon" times its derivative variable. Run the procedure once and keep the result. Reset the inputs, this time without the "epsilon" modification, and run again. Then evaluate the difference of outputs, divided by "epsilon". It is the sum of all columns of the Jacobian. For instance, if you want all inputs to be independent and all outputs to be dependent, and setting "ddeps" the epsilon, your code could now look like:


       ... whatever code is before ... 
C Initialize the derivatives of the independent and dependent parameters
C (don't forget to declare these variables !):
       x1d = 1.0
       x2d = 1.0
       ... 
       y1d = 0.0
       y2d = 0.0
       ... 
C Save what is necessary in the current state
       CALL SAVE_NECESSARY_PARAMS(x1, x2,..., y1, y2,...)
C Modify the current state:
       ddeps = 1.d-5
       x1 = x1 + ddeps*x1d
       x2 = x2 + ddeps*x2d
       ... 
C Call F(X + epsilon*Xd)
       CALL MYFUNC(x1, x2,..., y1, y2,...)
       res1_y1 = y1
       res1_y2 = y2
       ... 
C Prepare for the second run
       CALL RESTORE_NECESSARY_PARAMS(x1, x2,..., y1, y2,...)
C Call F(X)
       CALL MYFUNC(x1, x2,..., y1, y2,...)
       res2_y1 = y1
       res2_y2 = y2
       ... 
C Compute approx_Yd = (F(X+epsilon*Xd) - F(X))/epsilon
       approx_y1d = (res1_y1 - res2_y1)/ddeps
       ... 
       make sure these derivatives make sense! 
C End of the function I want to differentiate
       ... whatever code comes after ...

Validation of the differentiated programs

Help, the differentiated program crashes!
How can I be sure that the differentiated program really computes what I want?
How can I check the derivatives and find the place where the differentiated program goes wrong?

Since 2017, Tapenade supports validation and debug in a more automated way. The principles and implementation detail of validation and debug don't change much. You may take a look at them here, but our hope is that you might be able to validate the differentiated code without going too deep in these implementation details.
For short, divided differences are used to validate or to debug tangent AD, and then the correct tangent AD is used to validate or to debug adjoint AD. Specifically, debugging allows you to apply the validation test at a finer grain

Still, validation is not obvious, and debugging is even harder. The methods we will describe use Tapenade options that are available only in the command-line version (local installation). They require files provided in the ADFirstAidKit directory of your Tapenade installation. If you don't have a locally installed Tapenade, please follow these steps. Also, to ease our validation mechanism, we strongly advise you to follow a few preparation steps, before you even start to differentiate anything. Although we try to automate the process, validation and debug still require good knowledge of the principles of AD, especially for the adjoint mode. The sad thing with Tapenade's debugging mechanism is that while you are searching for bugs of Tapenade itself (otherwise you wouldn't be reading this section anyway!), you may also run into bugs of the validation mechanism itself.

In the following, actual pieces of code or commands are written in this sort of dark red. In those, <ADFirstAidKit> stands for the location of the ADFirstAidKit in your Tapenade installation.
For the sake of clarity, listings and commands are shown for a C source, but the descriptions below equally apply to Fortran sources: replace of course file1.c, file2.c, file3.c... with file1.f, file2.f, file3.f... (or ".f90" if appropriate), and replace gcc with your Fortran compiler. Similarly for the Tapenade-generated codes replace e.g. program_d.c with program_d.f. All utility files from the ADFirstAidKit remain the same.

The choice of Independent and Dependent parameters may interfere with the validation process. This is explained at the end of this section, but we'd rather warn you right now. Make sure you read this part if validation fails close to the entry-into or exit-from your code.

There exist specific Validation and Debugging processes for Tangent AD and for Adjoint AD. Validation only tests whether the derivative code produces correct derivatives. If the derivatives are wrong, you will need to go to Debugging, which is described after Validation for each of Tangent or Adjoint AD.
Tapenade's automated Validation and Debugging require the complete source, up to and including the PROGRAM or main() procedure. As usual, the source may perform calls to external procedures (e.g. libraries), the source of which you don't have or don't want to show to Tapenade (see black-box mechanism). Automated validation and debugging are fine with that. On the other hand, the wrapper or "context" code that eventually calls the code to differentiate (the "differentiation root") must be shown to Tapenade.

The primitives needed for Validation are defined in file adContext.c, provided in the ADFirstAidKit. If the code uses MPI, adContext.c should be replaced with adContextMPI.c, also provided in the ADFirstAidKit. In both cases, the associated header file is adContext.h
The primitives needed for Debugging are defined in file adDebug.c, provided in the ADFirstAidKit. If the code uses MPI, adDebug.c should be replaced with adDebugMPI.c, also provided in the ADFirstAidKit. For both, the associated header file is adDebug.h. Previous versions of Tapenade provided/used a adDebug.f, which should be considered obsolete now.

In our illustration example, we assume the "differentiation root" is some procedure P. We will call parameters of P the collection of all the variables used by P to communicate with its callers: these may be call arguments, result, globals, variables in COMMON, Module variables, Class fields (coming soon...). The independant inputs X and the dependent outputs Y are subsets of the parameters of P, chosen by the end-user. They may intersect. The code given to Tapenade, complete with PROGRAM or main(), is contained in a few files, say, file1.?, file2.?, file3.?. The language extensions ? depend on your code (c,f,f90...)

VALIDATION AND DEBUGGING FOR TANGENT AD:

Tangent Validation Differentiation:
Automated validation is triggered by adding the Tapenade command-line options -context and -fixinterface as follows (the order of options shouldn't matter):


$> tapenade -d -context -fixinterface -head "P(Y)/(X)" file1.c file2.c file3.c -o program

Option -fixinterface is not strictly necessary for validation of the tangent, but it will be if you proceed later to validation of the adjoint. You will notice that the produced program_d.c is complete with its own, new PROGRAM or main() procedure, and that the code locations where P_D is called are instrumented for the validation test. The produced code that lies "between" main() and P_D is mostly a copy or the original "context" code, except that it performs administrative operations such as declaration, allocation, initialization, or deallocation of derivative objects used by P_D.

Tangent Validation Principle:
Validation will compute divided differences (not centered) and compare them with tangent derivatives. Divided differences are obtained by two executions of the primal code:

One execution runs the tangent differentiated code on slightly perturbed values for the independents X+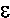*Xd. The values of Xd are chosen at random. Upon exit from P_D, a "Condensed perturbed result" is printed, which is Yb*Y for some arbitrary random Yb. The tangent derivative results Yd are not used.
The other execution runs the same tangent differentiated code, this time on X, with the same random Xd. Upon exit from P_D will be printed
-- a "Condensed result", which is Yb*Y for the same random Yb, and
-- a "Condensed tangent", which is Yb*Yd for the same random Yb.

Tangent Validation Execution:
Compile the tangent code produced by Tapenade, then run it twice, as follows. The shell variable DBAD_PHASE is used to distinguish the two runs. The file adContext.c is provided in the ADFirstAidKit


$> gcc -g -I <ADFirstAidKit> program_d.c <ADFirstAidKit>/adContext.c -lm -o tgt
$> export DBAD_PHASE=1 ; ./tgt
$> export DBAD_PHASE=2 ; ./tgt

The output should look like that (interspersed in the normal output of your code, shown as ... )


$> export DBAD_PHASE=1 ; ./tgt
... 
Perturbed run, seed=8.7e-01, epsilon=1.0e-08
=============================================
... 
[seed:8.7e-01] Condensed perturbed result :   3.1471183984092349e+01 (epsilon:1.0e-08)
... 
$> export DBAD_PHASE=2 ; ./tgt
... 
Tangent code,  seed=8.7e-01
=============================================
... 
[seed:8.7e-01] Condensed result :   3.1471183977980768e+01
[seed:8.7e-01] Condensed tangent:   6.1115750311254535e-01
...

The divided difference of the two condensed results should approximate the condensed tangent:


(3.1471183984092349e+01 - 3.1471183977980768e+01)/1.0e-08  => 6.111581e-01

Seems about right!
You may want to modify the arguments to the call to adContextTgt_init(1.d-8, 0.87d0) in program_d.c. The first argument is the divided difference's epsilon, the second argument is the seed for the random generation of Xd and Yd.

Tangent Debugging Differentiation:
Call Tapenade in tangent mode, with both command-line options -context -fixinterface and -debugTGT (the order of options shouldn't matter):


$> tapenade -d -context -fixinterface -debugTGT -head "P(Y)/(X)" \
    file1.c file2.c file3.c -o program_debugtgt

Again, you must show Tapenade the source complete with PROGRAM or main(). In our example case, we obtain a program_debugtgt_d.c

Tangent Debugging Principle:
You will need to run two executions of the differentiated code, in parallel. This can be done by calling the differentiated code from two different windows/shells.

One execution runs the tangent differentiated code on X+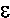*Xd. The values of Xd are chosen at random. At selected times/locations during execution, the current values of the active variables are sent to a FIFO buffer.
One execution runs the tangent differentiated code on X and on the same random Xd. At the corresponding times/locations during execution, the perturbed values of the active variables are read from the FIFO buffer and compared with this execution's values to compute their approximate tangent derivatives. Those are compared with the AD tangent derivatives. If they differ by more than a given threshold, a message is printed.

Tangent Debugging Execution:

For demo purposes, we have introduced an error into the tangent program i.e. here into program_debugtgt_d.c

Compile the tangent code produced by Tapenade. The file adDebug.c is provided in the ADFirstAidKit. Notice that file adStack.c is required too


$> gcc -g -I <ADFirstAidKit> program_debugtgt_d.c <ADFirstAidKit>/adDebug.c \
    <ADFirstAidKit>/adStack.c -lm -o tgt_debug

Execute the tangent code twice in parallel, in two different windows/shells:

Window 1:


$> export DBAD_PHASE=1 ; ./tgt_debug
... 
Starting TGT test, phase one, epsilon=1.0e-08 [seed=8.7e-01]
==========================================
... 
==========================================
...

Window 2:


$> export DBAD_PHASE=2 ; ./tgt_debug
... 
Starting TGT test, phase two, epsilon=1.0e-08 [seed=8.7e-01]
==========================================
... 
==========================================
Condensed tangent:   -1.4937102974828314e+00 (ad)140.9% DIFF WITH (dd)  6.1115837013403507e-01 [seed:8.7e-01]
...

In the rest of this section, we will not show "Window 1" any more because it will not change much, but it is still there! Remember that for each debugging run, you need to run tgt_debug in Window 1 (with DBAD_PHASE=1) and in Window 2 (with DBAD_PHASE=2), as they are waiting for each other to run.

So far, we haven't learned much, and validation told us the same: there's something wrong in the tangent differentiated code! Let's now try to narrow in on the bug. The code program_debugtgt_d.c produced through the -debugTGT option is equipped with debugging primitives at many locations, but they are by default inactive. To activate them, we are going to carefully modify program_debugtgt_d.c. In program_debugtgt_d.c, immediately before the call to the differentiated root P_D, we find the call
adDebugTgt_call("P", 0, 0)

Argument 2 is an additional debugging depth d2: if nonzero, an additional d2 call tree levels under this call will be debugged.
Argument 3 is an absolute debugging depth d3: if nonzero, exactly d3 call tree levels under this call will be debugged.

Therefore, if we modify to, say, adDebugTgt_call("P", 2, 0) and compile again (no need to differentiate again!), execution outputs become:

Window 2:


$> export DBAD_PHASE=2 ; ./tgt_debug
Starting TGT test, phase two, epsilon=1.0e-08 [seed=8.7e-01]
===========================================================
  [ 1]AT:entry OF P
    [ 2]AT:entry OF polyperim
perim   1.5468877734292619e+00(dd  70.1% DIFF WITH ad)  5.1742590489108133e+00
    [ 2]AT:exit OF polyperim
    [ 2]AT:entry OF polysurf
    [ 2]AT:exit OF polysurf
result2   3.2682265782568720e-01(dd  95.5% DIFF WITH ad)  7.3417226991307531e+00
  [ 1]AT:exit OF P
cost   3.2682265782568720e-01(dd  95.5% DIFF WITH ad)  7.3417226991307531e+00
===========================================================
Condensed tangent:   1.3729021447374508e+01 (ad) 95.5% DIFF WITH (dd)  6.1115837013403507e-01 [seed:8.7e-01]

The execution in Window 1 didn't print more useful info. On the other hand Window 2 displays more steps of the computation, namely the entry and exit points to all procedure calls up to call depth 2. Between each sucessive steps, execution checks the values of derivatives and prints a message only if there is a discrpancy. On the example, we see that the derivative of variable perim is in trouble, with an estimate divided difference of 1.54 and a computed tangent of 5.17. The problem occured somewhere between the entry into procedure polyperim (since nothing was signalled wrong before) and the exit from polyperim. The error was detected at the procedure's exit, but of course it may originate from anywhere inside. Later errors (on result2 and cost) are hopefully consequences of the first error, so we will leave them aside for the time being.

To investigate further, we may again modify the investigation depth in adDebugTgt_call("P", 2, 0), replacing 2 with 3. This may make the investigated call tree grow a lot. We may instead leave the "2", or even make it a "1", and then find the adDebugTgt_call("polyperim", 0, 0) in P_D and replace its first "0" with a "1". This way we can select precisely the branch of the call tree that we want to examine.

An alternative is to use the third argument of a adDebugTgt_call("polyperim", 0, 0). This number is an absolute investigation depth below the current call, and it is triggered even if the current call is so deep that it was not investigated itself. Let's do this and make it a "2".

If we just compile again, execution outputs become:

Window 2:


$> export DBAD_PHASE=2 ; ./tgt_debug
Starting TGT test, phase two, epsilon=1.0e-08 [seed=8.7e-01]
===========================================================
    [ 2]AT:entry OF polyperim
      [ 3]AT:entry OF incrsqrt
pp   7.0710690636133222e-01(dd  55.4% DIFF WITH ad)  1.5839191898578668e+00
      [ 3]AT:exit OF incrsqrt
pp   7.0710690636133222e-01(dd  55.4% DIFF WITH ad)  1.5839191898578668e+00
      [ 3]AT:entry OF incrsqrt
  ......Many similar lines deleted...... 
      [ 3]AT:exit OF incrsqrt
perim   1.5468877734292619e+00(dd  70.1% DIFF WITH ad)  5.1742590489108133e+00
    [ 2]AT:exit OF polyperim
cost   3.2682265782568720e-01(dd  95.5% DIFF WITH ad)  7.3417226991307531e+00
===========================================================
Condensed tangent:   1.3729021447374508e+01 (ad) 95.5% DIFF WITH (dd)  6.1115837013403507e-01 [seed:8.7e-01]

Now we see the problem lies inside procedure incrsqrt: the derivative of its output variable pp is wrong. To investigate further, we may either probe for selected variables, anywhere we want inside incrsqrt. For example inserting somewhere inside incrsqrt_d:


adDebugTgt_testReal8("xx2", xx2, xx2d);

will test the derivatives of scalar double variable xx2 at that location. Similarly:


adDebugTgt_testReal4Array("someArray", someArray, someArrayd, 10);

will test the derivatives of the array of single precision (float) values someArray, for its 10 first elements. You may test individual element references as you please:


adDebugTgt_testReal8("Field_y_of_T_42", T[42]->y, Td[42]->y);

A more systematic alternative is to ask Tapenade to insert those. To this end, insert directives in the primal source:


$AD DEBUG-HERE befsqrt true true

will insert into the differentiated code, at this location, a test for the derivatives of every variable which is active there. The first directive argument (here befsqrt) will be used in the output to identify this location. The syntax of Tapenade directives varies with the language. Playing with these levers to pilot the debugging code, we can eventually obtain something like:

Window 2:


$> export DBAD_PHASE=2 ; ./tgt_debug
Starting TGT test, phase two, epsilon=1.0e-08 [seed=8.7e-01]
===========================================================
xx2   3.1200002581499575e+00(dd  70.5% DIFF WITH ad)  1.0560000000000000e+01
xx2  -5.1999995420715095e-01(dd 113.9% DIFF WITH ad)  3.7399999999999998e+00
xx2   2.6000002151249646e-01(dd  77.0% DIFF WITH ad)  1.1299999999999999e+00
xx2   1.0400000860499858e+00(dd  93.7% DIFF WITH ad)  1.6520000000000000e+01
cost   3.2682265782568720e-01(dd  95.5% DIFF WITH ad)  7.3417226991307531e+00
===========================================================
Condensed tangent:   1.3729021447374508e+01 (ad) 95.5% DIFF WITH (dd)  6.1115837013403507e-01 [seed:8.7e-01]

Now we know the faulty variable and the line where it goes wrong. With a little luck, this will be the place where the bug lies.
To be totally honest, this debugging mechanism is far from bullet-proof. It is still under constant development or debugging. One problem is false positives: sometimes because of the choice of the divided differences epsilon, the divided difference can deviate a lot from the derivative, thus triggering a message during debugging. Comparing divided differences with tangent derivatives is also quite delicate when one is exactly zero whereas the other is not. There's a lot more to say about all that. If you are interested, feel free to look at the sources of adDebug.c, we welcome every suggestion for improvement!

VALIDATION AND DEBUGGING FOR ADJOINT AD: (Assuming tangent AD is now correct !)

Adjoint Validation Differentiation:
Add command-line options -context and -fixinterface to your adjoint differentiation command as well:


$> tapenade -b -context -fixinterface -head "P(Y)/(X)" file1.c file2.c file3.c -o program

Again, you must show Tapenade the source complete with PROGRAM or main(). Option -fixinterface is needed since we will compare adjoint derivatives with tangent derivatives: we must prevent Tapenade from refining the sets of independents and dependents (here X and Y), leading to different validation results in tangent and adjoint.

Adjoint Validation Principle:
Validation needs only one run of the adjoint code. This run will use the same input X and the same Yb as the weightings of the dependent outputs. Upon exit from P_B the adjoint run should normally produce an adjoint Xb. At that point, a "Condensed adjoint" will be printed, which is Xb*Xd, for the same randomly chosen Xd as for tangent validation. By definition of the adjoint, this should be equal to the Condensed tangent Yb*Yd.

Adjoint Validation Execution:
Compile the tangent code produced by Tapenade and run it. The shell variable DBAD_PHASE doesn't matter for adjoint validation. The file adContext.c is needed again, together with the usual adStack.c. These files are provided in the ADFirstAidKit.


$> gcc -g -I <ADFirstAidKit> program_b.c <ADFirstAidKit>/adContext.c \
    <ADFirstAidKit>/adStack.c -lm -o adj
$> ./adj

The output should look like that (interspersed in ... the normal output of your code)


$> ./adj
... 
Adjoint code,  seed=8.7e-01
===================================
[seed:8.7e-01] Condensed adjoint:   6.1115750311254413e-01
...

The condensed adjoint should be equal to the condensed tangent, up to machine precision. Notice that the output of your code after the printing or the condensed adjoint may differ from the original. Your code may even crash after that point. This is a normal consequence of the adjoint validation process that alters the original output of the differentiation root.

Adjoint Debugging Differentiation:
Differentiate in adjoint mode and in tangent mode, with both command-line options -context -fixinterface and -debugADJ (the order of options shouldn't matter):


$> tapenade -d -context -fixinterface -debugADJ -head "P(Y)/(X)" \
    file1.c file2.c file3.c -o program_debugadj
$> tapenade -b -context -fixinterface -debugADJ -head "P(Y)/(X)" \
    file1.c file2.c file3.c -o program_debugadj

Again, you must show Tapenade the source complete with PROGRAM or main(). In our example case, we obtain a program_debugadj_d.c and a program_debugadj_b.c. They are both specialized for, and necessary for adjoint debugging. In particular this program_debugadj_d.c is very different from the program_debugtgt_d.c of Tangent debugging.

Adjoint Debugging Principle:
You will need to run the "debugadj" adjoint (program_debugadj_b.c) in parallel with the "debugadj" tangent (program_debugadj_d.c). The "debugadj" adjoint will regularly send a checksum of its adjoint derivatives, and the "debugadj" tangent will receive those and compare them with the checksum of its derivatives. For each pair of corresponding sections of program_debugadj_b.c and program_debugadj_d.c (i.e. coming from the same section of the original primal code):

at the beginning of each section in program_debugadj_b.c (which actually corresponds to the section exit in the primal code, yes, this is reverse mode), the values of the adjoint derivatives are set to some Yb chosen pseudo-randomly. At the end of this section in program_debugadj_b.c, the resulting Xb are multiplied (dot-product) with a Xd chosen pseudo-randomly and the result is sent to a special stack. Then the process repeats for the next sections till the program terminates.
at the beginning of each section in program_debugadj_d.c, the values of the derivatives are set to the same Xd as at the end of the corresponding section in program_debugadj_b.c. At the end of this section in program_debugadj_d.c, the resulting Yd are multiplied (dot-product) with the same Yb as at the beginning of the corresponding section in program_debugadj_b.c. The result is compared to the value popped from the special stack, error messages are sent if necessary, and the process repeats for the next sections till the program terminates.

Adjoint Debugging Execution:

For demo purposes, we have introduced an error into the adjoint program i.e. here into program_debugadj_b.c

First compile both differentiated codes:


$> gcc -g -I <ADFirstAidKit> program_debugadj_b.c <ADFirstAidKit>/adDebug.c \
    <ADFirstAidKit>/adStack.c -lm -o adj_debug1
$> gcc -g -I <ADFirstAidKit> program_debugadj_d.c <ADFirstAidKit>/adDebug.c \
    <ADFirstAidKit>/adStack.c -lm -o adj_debug2

(Fortran note: in Fortran, the adjoint code in program_debugadj_b.f may not include copies of the primal procedures, and may need some of them. You may have to link the first compilation above with a part of your primal code. This seems incoherent with what happens in C, and may be fixed in the future...)

Then execute in two different windows/shells:

Window 1:


$> export DBAD_PHASE=1 ; ./adj_debug1
... 
Starting ADJ test, phase one (bwd), errmax= 0.1% [seed=8.7e-01] 
=========================================================== 
...

Window 2:


$> export DBAD_PHASE=2 ; ./adj_debug2
Starting ADJ test, phase two (fwd), errmax= 0.1% [seed=8.7e-01]
===========================================================
[ 0]AT:start OF TESTED CODE
                         200.0% DIFFERENCE!!  tgt:  6.1115750311254535e-01  adj: -2.1575612270916129e+00
[ 0]AT:end OF TESTED CODE
End of ADJ test, 1 error(s) found.
===========================================================
...

In the rest of this section, we will not show "Window 1" any more because it will not change much, but it is still there! Remember that for each debugging run, you need to run adj_debug1 in Window 1 and adj_debug2 in Window 2, as they are waiting for each other to run.

Again, to learn more we need to go to deeper detail in the call tree. The two differentiated programs are equipped with "boundaries" at

The entry into and exit from each active (i.e. differentiated) procedure
Some middle point in each active procedure (most ofter, except if procedure is too small)
Additional points designated (by the end-user in the source primal code) by the directives
```
$AD DEBUG-HERE <locationName> true true
```
that we already mentioned for tangent debugging.

These boundaries delimitate the debugging sections that we mentioned in the Adjoint Debugging Principle above. By default, these boundaries are deactivated, and you may activate them by modifying the 2nd argument of the calls


adDebugBwd_call(<procedureName>, 0);

in program_debugadj_b.c (don't modify program_debugadj_d.c). You may also activate the boundaries other than procedure entry or exit by changing the first "boolean" value in the tests


if (0 && adDebugBwd_here(<boundaryName>))

in program_debugadj_b.c. Be aware that the place where you may play with these boundaries is in program_debugadj_b.c that is, in the backward sweep of the adjoint code. Consequently boundaries appear in a reversed, unnatural order. This may cause a few headaches!

Unfortunately, compared to tangent debugging we have fewer levers to narrow in to the bug location:

The 2nd argument of
```
adDebugBwd_call(<procedureName>, 0);
```
is the additional investigation depth under the present call. Unlike in tangent debugging, there is no absolute investigation depth (the 3rd argument): once debugging is deactivated for a given call, it cannot be activated again somewhere under this call.
boundaries inside a given procedure cannot be activated if the procedure's entry and exit are deactivated.
one cannot focus on selected variables: in each debugging section (i.e. between two successive boundaries), the test compares the checksum of all derivatives as a whole.

That said, with the few levers that we have, we still can narrow in on the bug location. Here for instance, we have set the investigation depth to "3" on


adDebugBwd_call(P, 3);

and obtained the output:

Window 2:


$> export DBAD_PHASE=2 ; ./adj_debug2
Starting ADJ test, phase two (fwd), errmax= 0.1% [seed=8.7e-01]
===========================================================
[ 0]AT:start OF TESTED CODE
  [ 1]AT:entry OF P
    [ 2]AT:entry OF POLYPERIM
      [ 3]AT:entry OF INCRSQRT
      [ 3]AT:befsqrt OF INCRSQRT
                          18.3% DIFFERENCE!!  tgt:  4.2351784051238548e+00  adj:  3.5255496097510757e+00
      [ 3]AT:exit OF INCRSQRT
      [ 3]AT:entry OF INCRSQRT
      [ 3]AT:befsqrt OF INCRSQRT
                          34.9% DIFFERENCE!!  tgt:  5.0630250000000006e+00  adj:  3.5576750000000006e+00
      [ 3]AT:exit OF INCRSQRT
      [ 3]AT:entry OF INCRSQRT
      [ 3]AT:befsqrt OF INCRSQRT
                          24.8% DIFFERENCE!!  tgt:  4.5409833333333331e+00  adj:  3.5374166666666675e+00
      [ 3]AT:exit OF INCRSQRT
      [ 3]AT:entry OF INCRSQRT
      [ 3]AT:befsqrt OF INCRSQRT
                          23.7% DIFFERENCE!!  tgt:  4.4874044201062411e+00  adj:  3.5353374849593475e+00
      [ 3]AT:exit OF INCRSQRT
      [ 3]AT:entry OF INCRSQRT
      [ 3]AT:befsqrt OF INCRSQRT
                          15.8% DIFFERENCE!!  tgt:  4.1233500000000003e+00  adj:  3.5212100000000008e+00
      [ 3]AT:exit OF INCRSQRT
    [ 2]AT:exit OF POLYPERIM
    [ 2]AT:entry OF POLYSURF
    [ 2]AT:exit OF POLYSURF
  [ 1]AT:exit OF P
[ 0]AT:end OF TESTED CODE
End of ADJ test, 5 error(s) found.
===========================================================

This tells us that the bug lies somewhere in INCRSQRT, after the intermediate boundary named befsqrt. We can then use a few additional boundaries inside this procedure to focus on the faulty lines.
Even more than for tangent debugging, we must admit adjoint debugging has many shortcomings (euphemism for bugs). To name just a few:

in C, debug routines on C arrays (i.e. adDebugAdj_(r|w|rw)Real(4|8)Array) are sometimes wrongly replaced by adDebugAdj_(r|w|rw)Real(4|8). The reason is that a C pointer can be just a pointer to an object, or a pointer to the beginning of an array. When Tapenade cannot tell, it supposes the 1st case (plain pointer to an object) and thus forgets about the rest of the array. The problem is (should be) pointed out by message (AD15) "Not sure how to ...". Of course this can make things go very wrong, so you should check and modify the generated code when necessary
The test on the returned value (in C) is sometimes missing (bug, to be fixed)
Turning debugging on (with option -debutTGT or -debutADJ) slightly changes the policy about when the derivatives of passive pariables are set to zero. Although this in general turns one cause of bugs off, we have observed cases where some of these initializations go missing! This is a bug on our TODO list, and until we fix it, it doesn't hurt to add these initializations by hand. In particular if the adjoint produces NaN's, you may want to explicitly initialize to zero all derivative variables when they come into scope.

Suggestions for improvement welcome!

PROBLEMATIC INTERACTION WITH INDEPENDENT AND DEPENDENT PARAMETER SETS:

This problem was identified and studied with the help of Nicolas Huneeus, LSCE-IPSL, University of Versailles Saint-Quentin.
Tapenade sometimes takes the liberty to modify the Independent and Dependent parameters provided by the end-user. The reasons are described here and, although they are complex, we believe they are justified. This modification can be different in tangent and adjoint modes.

This may cause problems in the tangent validation ("divided differences") because it affects the way derivatives are initialized.
This will certainly cause problems in the adjoint validation ("dot product") if the tangent and adjoint codes are built with (in)dependent paramaters that don't match

As a result, the validation results may display unjustified "Differences", located at the entry or at the exit of the head procedure.

The sign you must look for is the occurrence of one of the messages:
Command: Input variable(s) xxxx have no differentiable influence in pppp: removed from independents
Command: Output variable(s) xxxx are not influenced differentiably in pppp: removed from dependents
Command: Input variable(s) xxxx have their derivative modified in pppp: added to independents
Command: Output variable(s) xxxx have their derivative modified in pppp: added to dependents
when setting the message level high enough (command-line option -msglevel 20).

There are two ways to turn around this problem:

either add the command-line option -fixinterface and the Independent and Dependent parameters will not be modified,
or modify by hand your Independent and Dependent parameter sets, according to the variables indicated by the above messages. Then the sets will be coherent again between the tangent and the adjoint codes.

Independent and Dependent sets. Initialization and usage of the differentiated parameters

What variables should I list in the "-vars" and "-outvars" arguments of the differentiation command? (also known as the independent and dependent parameters)
Also related: for my root procedure, the differentiated procedure that I obtain has additional differentiated parameters.
What value should I give to these variables upon calling the differentiated root procedure?
What value will I obtain in these variables upon return?

To begin with, what we refer to as "parameters" here is not limited to formal parameters in the procedure's argument list. The following applies just as well to global parameters such as those in a COMMON or in the variables of a USE'd module. If these variables are active, differentiated variables will appear close to them, and if these active variables are inputs or outputs, you will have to think about providing their initial value and retrieving their result value.

Now some notation. Suppose we are calling Tapenade on some root procedure F, and call V some parameter of F. Although we advocate differentiating in a single batch all the subroutines that define the mathematical function of interest, it may help in the following explanation to think of F as only a part of this big mathematical function. Then in general there may be some upstream code U that runs before F is called, and some downstream code D that runs after F is called. The complete mathematical function is implemented by {U; F; D}. This code sequence has an input that we call the "main entry", and an output that we call the "main result". The general goal is to compute the derivatives of the main result with respect to the main entry. Assuming that U and D are also differentiated in some way, the questions are: should V go into the independent and dependent sets, what is the new parameter Vd (or Vb) of the differentiated F_D (or F_B), what value should be provided into it, and what value will it contain upon exit? The header of each differentiated root procedure answers some of these questions. However, some explanations may be useful.

Question 1: What should the independent and dependent parameters be set as?

It is wise not to think of those as the sets of inputs and outputs of F that are connected differentiably through F. Tapenade can find this by itself !
What Tapenade does expect from you is information about the context outside F. As a rule of thumb:

Think of the independents as the inputs of F that are influenced by the "main entry", i.e. that are differentiably connected to the main entry through U. In the degenerate case where there is no U (empty U), the independents must be the inputs of F for which you, the end-user, promise to give a tangent derivative or expect a reverse derivative.
Think of the dependents as the outputs of F that influence the "main result", i.e. that are differentiably connected to the main result through D. In the degenerate case where there is no D (empty D), the dependents must be the outputs of F for which you, the end-user, expect a tangent derivative or promise to give a reverse derivative.

For example, if the context outside F is

 U(in:a,out:b); F(in:b,out:c); D(in:b,in:c,out:d);

b is used differentiably later in D. Therefore, even if F only reads b and does not modify it, b must be in the set of dependents.
Another possible mistake comes with loops. If the code looks like

 U(in:a,out:b); loop {F(in:b,out:c);} D(in:c,out:d);

the downstream code after F includes F itself, because of the loop, and therefore b must be in the dependents.

Please notice that Tapenade may remove variables from the independents or dependents sets that you provided. Tapenade detects superfluous independents, i.e. inputs that have no differentiable influence on any dependent. Similarly a superfluous dependent is an output that doesn't depend differentiably on any independent and isn't independent itself. Superfluous variables are removed from their set, and a "command" message is issued. If you don't specify any independents (resp. dependents), Tapenade chooses for you the largest possible set, using its dependence analysis to remove superfluous elements.

There are also situations where Tapenade adds variables to the independent or dependent sets that you provided for a root procedure. In tangent mode, if V is in the independent set and Vd may be overwritten in F_D, then V is added into the dependent set. Conversely in reverse mode, if V is in the dependent set and Vb may be overwritten in F_B, then V is added into the independent set. In both cases a "command" message is issued. This is Tapenade's way of warning the end-user that, although V was not in the dependent (resp. independent) set provided, the original Vd (resp. Vb) provided will be modified by the derivative procedure, and therefore will loose its original value and should be used with care after that.

Question 2: What is the effect of a variable being in the independent and/or dependent sets, on the required initialization and returned value of its derivative?

Whatever independents and dependents sets you provided, it is wise to check these sets modified and actually used by Tapenade, as listed in the comment header of the differentiated procedure. These sets determine how the derivatives must be initialized and what they will contain upon exit. This information is also summarized in the comment header of every differentiated root procedure.

The following table shows and explains the possible cases. In tangent mode, things are straightforward. In reverse mode things prove a little more surprising, but they are "logical" consequences of the transposition of the Jacobian matrix that is behind the reverse mode. To give a rough idea, in reverse mode the flow of data goes in the reverse direction: If V is an output of F, then F_B must be called with an additional input VB, and conversely if V is an input of F, then F_B will return an additional output VB. When a variable is purely read by F, its derivative is purely incremented (and vice versa)... oh yes, you're right it's complicated! But we never said that the reverse mode is simple, it's only extremely efficient and worth the effort!

If `V` is listed as ...	then in tangent mode, `Vd`...	then in reverse mode, `Vb`...
... an independent (i.e. "`varying`") input only	... is a required input, and an unspecified output. Upon entry, `F_D` expects a value in `Vd`, which should be in general the derivative of `V` upon `F` entry with respect to the "main entry". In the particular case where this derivative is null, it is the responsibility of the calling context to set `Vd` to `0.0` before the call to `F_D`. Depending of what `F` does to `V`, `Vd` may very well be modified by `F_D`: since `V` is not in the dependent outputs, the value of `Vd` upon `F_D` exit has no meaning and should not be used. This is ok if `V` upon `F` exit has no influence on the "main result". When `F` is a differentiation root procedure, this appears in the RW status in the header of `F_D` as "`V:in`" or "`V:in-killed`" to stress when `Vd` is modified by `F_D`.	... is a result only. Upon `F_B` exit, `Vb` contains the derivative of the "main result" with respect to the `V` upon `F` entry. This is possible because `F_B` expects as input the derivative of the "main result" with respect to each of `F`'s dependent outputs. Since `V` is not in the dependent outputs, `F_B` expects no meaningful value provided at call time in `Vb`. Actually, whatever is in there will be happily discarded, reset to zero, and overwritten. Therefore its value upon `F_B` entry will be lost. When `F` is a differentiation root procedure, this appears in the RW status in the header of `F_B` as "`V:out`" or "`V:zero`" when the `Vb` is null upon return from `F_B`.
... a dependent (i.e. "`useful`") output only	... is a result only. Upon `F_D` exit, `Vd` contains the derivative of `V` upon `F` exit with respect to the "main entry". This is possible because `F_D` expects as input the derivatives of `F`'s independent inputs with respect to the "main entry". Since `V` is not in the independent inputs, the value of `Vd` upon `F` entry is meaningless. Actually, whatever is in there will be happily discarded and overwritten, Therefore its value upon `F_D` entry will be lost. When `F` is a differentiation root procedure, this appears in the RW status in the header of `F_D` as "`V:out`" or "`V:zero`" when the exit `Vd` is null.	... is a required input, and an unspecified output. Upon entry, `F_B` expects a value in `Vb`, which should be in general the derivative of the "main result" with respect to `V` upon `F` exit. In the particular case where this derivative is null, it is the responsibility of the calling context to set `Vb` to `0.0` before the call to `F_B`. Depending of what `F` does to `V`, `Vb` may very well be modified by `F_B`: since `V` is not in the independent inputs, the value of `Vb` upon `F_B` exit has no meaning and should not be used. This is ok if `V` upon `F` entry does not depend on the "main entry". When `F` is a differentiation root procedure, this appears in the RW status in the header of `F_B` as "`V:in`" or "`V:in-killed`" to stress when `Vb` is modified by `F_B`.
... independent and dependent	... is a required input and a result. Upon entry, `F_D` expects a value in `Vd`, which should be in general the derivative of `V` upon `F` entry with respect to the "main entry". In the particular case where this derivative is null, it is the responsibility of the calling context to set `Vd` to `0.0` before the call to `F_D`. Upon `F_D` exit, `Vd` contains the derivative of `V` upon `F` exit with respect to the "main entry". This is possible because `F_D` expects as input the derivatives of `F`'s independent inputs with respect to the "main entry". When `F` is a differentiation root procedure, this is summarized in the RW status of `V` in the header of `F_D`. This status can start with "`in`" when the entry value of `Vd` is used, and continues with "`out`" when `Vd` is modified by `F_D` "`zero`" when `Vd` is reset to zero by `F_D` or nothing when `Vd` is not modified by `F_D`	... is a required input and a result. Upon entry, `F_B` expects a value in `Vb`, which should be in general the derivative of the "main result" with respect to `V` upon `F` exit. In the particular case where this derivative is null, it is the responsibility of the calling context to set `Vb` to `0.0` before the call to `F_B`. Upon `F_B` exit, `Vb` contains the derivative of the "main result" with respect to the `V` upon `F` entry. This is possible because `F_B` expects as input the derivative of the "main result" with respect to each of `F`'s dependent outputs. When `F` is a differentiation root procedure, this is summarized in the RW status of `V` in the header of `F_B`. This status can start with "`in`" when the entry value of `Vb` is used, and continues with "`out`" when `Vb` is modified by `F_B` "`zero`" when `Vb` is reset to zero by `F_B` or nothing when `Vb` is not modified by `F_B` The RW status can also be "`incr`", meaning that `Vb` is simply incremented and not otherwise read nor written by `F_B`.

Example: consider for instance procedure F below, that should illustrate many of the possible situations.


      subroutine F(u2,v1,v3,w2)
      real u1,u2,u3,v1,v2,v3,w1,w2,w3
      common /cc/u1,u3,v2,w1,w3
c
      u3 = u3+v1*u1
      u3 = u3-u2*v2
      u2 = 3.0*u1*v1
      u3 = u3+G(u2)
c
      v3 = v3+2.0*v1
      v3 = v3-v2
      v2 = 3.0*v1
      v3 = v3+G(v2)
c
      w3 = w3+v1*v2
      w3 = w3-w2*u1
      w2 = 3.0*w1
      w3 = w3+G(w2)
      end

      real function G(x)
      real x
      G = x*x
      end

Function G is some pure user-defined function. We built this code so that all *1 parameters are only read by F, *2 parameters are read, then overwritten and maybe read again, and *3 parameters are only incremented, which is an interesting case for reverse differentiation. Parameters are scattered as formal arguments or global variables, just to show it doesn't matter.

Suppose that the end-user decided that all v* and w* parameters are independents, and all u* and w* are dependents, e.g. using the command-line option:


    -head "F(v1 v2 v3 w1 w2 w3)>(u1 u2 u3 w1 w2 w3)"

In tangent mode, procedure `F_D` is	In reverse mode, procedure `F_B` is
C Differentiation of f in forward (tangent) mode: C variations of useful results: u3 v2 w3 w2 u2 C with respect to varying inputs: v2 w1 w3 v1 w2 C RW status of diff variables: u3:out v2:in-out C w1:in w3:in-out v1:in w2:in-out u2:out SUBROUTINE F_D(u2, u2d, v1, v1d, v3, w2, w2d) IMPLICIT NONE C REAL u1, u2, u3, v1, v2, v3, w1, w2, w3 REAL u2d, u3d, v1d, v2d, w1d, w2d, w3d COMMON /cc/ u1, u3, v2, w1, w3 REAL G REAL G_D REAL result1 REAL result1d COMMON /cc_d/ u3d, v2d, w1d, w3d C u3d = u1v1d u3 = u3 + v1u1 u3d = u3d - u2v2d u3 = u3 - u2v2 u2d = 3.0u1v1d u2 = 3.0u1v1 result1d = G_D(u2, u2d, result1) u3d = u3d + result1d u3 = u3 + result1 C v3 = v3 + 2.0v1 v3 = v3 - v2 v2d = 3.0v1d v2 = 3.0v1 result1 = G(v2) v3 = v3 + result1 C w3d = w3d + v1dv2 + v1v2d w3 = w3 + v1v2 w3d = w3d - u1w2d w3 = w3 - w2u1 w2d = 3.0w1d w2 = 3.0w1 result1d = G_D(w2, w2d, result1) w3d = w3d + result1d w3 = w3 + result1 END	C Differentiation of f in reverse (adjoint) mode: C gradient of useful results: u3 w1 w3 w2 u2 C with respect to varying inputs: u3 v2 w1 w3 v1 C w2 u2 C RW status of diff variables: u3:in-out v2:out C w1:incr w3:in-out v1:out w2:in-out u2:in-out SUBROUTINE F_B(u2, u2b, v1, v1b, v3, w2, w2b) IMPLICIT NONE C REAL u1, u2, u3, v1, v2, v3, w1, w2, w3 REAL u2b, u3b, v1b, v2b, w1b, w2b, w3b COMMON /cc/ u1, u3, v2, w1, w3 REAL G REAL result1 REAL result1b COMMON /cc_b/ u3b, v2b, w1b, w3b CALL PUSHREAL4(u2) C u2 = 3.0u1v1 CALL PUSHREAL4(v2) C v2 = 3.0v1 C w2 = 3.0w1 result1b = w3b CALL G_B(w2, w2b, result1b) w1b = w1b + 3.0w2b w2b = -(u1w3b) v1b = v2w3b v2b = v1w3b CALL POPREAL4(v2) result1b = u3b CALL G_B(u2, u2b, result1b) v1b = v1b + u13.0u2b + u1u3b + 3.0v2b CALL POPREAL4(u2) u2b = -(v2u3b) v2b = -(u2u3b) END
You can see that Tapenade took `u1` and `w1` out of the set of dependents because they are not influenced differentiably by any independent. It also took `v3` out of the independents because it has no differentiable influence on any dependent and is not dependent itself. Also, Tapenade added `v2` to the set of dependents because its derivative has to be modified by `F_D`. Since `v1, v2, w1, w2`, and `w3` are independent (i.e. in the comment "`varying inputs`"), procedure `F_D` expects to be provided with their derivatives `v1d, v2d, w1d, w2d`, and `w3d` with respect to the "main entry". After modification of the independent and dependent sets by Tapenade, there is simply no `u1d` nor `v3d` since they are neither independent nor dependent. The value upon `F_D` entry of the other derivative variables `u2d` and `u3d` are meaningless and are happily overwritten inside `F_D`. So beware that whatever was in there before calling `F_D` may be lost. The dependent are variables `u2, u3, v2, w2`, and `w3` (i.e. in the comment "`useful results`"), so that they contain upon `F_D` exit the derivative of the corresponding original variable upon `F_D` exit with respect to the "main entry". Variables `u1, v1, v3`, and `w1` are not dependent, therefore the exit value of their derivative is not specified. In fact these derivatives are not overwritten so there is no risk. In other words, variables `u1, v1, v3`, and `w1` are only read inside `F` and therefore their derivatives either don't exist or are only read by `F_D`. They retain their input value.	You can see that Tapenade took `u1` out of the set of dependents because it is not influenced differentiably by any independent and it is not an independent itself. It also took `v3` out of the independents because it has no differentiable influence on any dependent and is not dependent itself. Also, Tapenade added `u2` and `u3` to the set of independents because their derivative has to be modified by `F_B`. Actually this is not the case for `u3` because `u3` is only incremented in `F`, but Tapenade does not detect this (yet?). Since `u2, u3, w1, w2`, and `w3` are dependent (i.e. in the comment "`useful results`"), procedure `F_B` expects to be provided with the derivatives `u2b, u3b, w1b, w2b`, and `w3b` of the "main result" with respect to them. After modification of the independent and dependent sets by Tapenade, there is simply no `u1b` nor `v3b` since they are neither independent nor dependent. The input values of the other derivatives `v1b` and `v2b` are meaningless and may be happily overwritten inside `F_B`. So beware that whatever was in there before calling `F_B` may be lost. At the other end of `F`, the independent are variables `u2, u3, v1, v2, w1, w2`, and `w3` ("`varying inputs`"). Therefore they contain upon exit from `F_B` the derivative of the "main result" with respect to their corresponding original variable, upon `F` entry. Notice furthermore that variables `u3` and `w3` are only incremented inside `F` and therefore their derivatives `u3b` and `w3b` are only read by `F_B`. They retain their input value. Still, Tapenade was not able to detect that and returned the more general RW status "`in-out`"

Location of declaration and creation/allocation of differentiated scalars and arrays

I see an inconsistency in the place where scalar derivatives and array derivatives are declared and allocated.
The derivative of a scalar is sometimes declared, not at the same location as the original scalar, but as a new local variable in some procedure that uses the original scalar.

There is a subtle difference. Derivative arrays may be hard to declare and allocate at some random location. Actually the only place where it is easy to do so is the location of declaration and allocation of the original, non-differentiated array. If we are near the declaration (resp. allocation) of the original array, then we have all size information at hand and we may use it identically for the declaration (resp. allocation) of the derivative array. Otherwise, the size information may be very hard to find. In some cases, we may even need to resort to a user-defined constant, which is an extra burden for the end-user, see ISIZE* constants.
In general, there is no such problem with scalars.

On the other hand, it's good to reduce the scope of derivative variables to exactly where they are used. This may reduce the memory occupation of the derivative program. This may also clarify the derivative program by explicitly focusing the place where the derivative is used.

Therefore the place where derivative variables are declared (resp. allocated) varies along with the variable type. It's not really inconsistent but it may be surprising. In general:

Derivatives of scalars and more generally those which are easily declared (resp. allocated) anywhere, are declared (resp. allocated) as close as possible to the place where they are used. It may thus happen that the derivative of a formal parameter of procedure FOO is a local variable of FOO_D or FOO_B.
Derivatives of unknown size or dynamic arrays, and more generally those which are hard to declare (resp. allocate) anywhere, are declared (resp. allocated) at the same location as their original variable, and passed along all the way to the place where they actually become useful (i.e. where the original becomes active).

Problems with web browsers (Macintosh):

I'm using Internet Explorer for Macintosh, and Tapenade complains about syntax errors in my Fortran files. However I'm sure the syntax is correct, and/or it works fine through the cut-and-paste interface.

This bug was found and fixed by David Pearson, University of Reading U.K. The reason might be that the Fortran files that you are uploading to us are sent as "application/x-macbinary" instead of "application/octet-stream". This can be fixed by modifying your browser's preferences:

Open "Preferences", then click either on "File Helpers" if visible, or on "Receiving Files/File Helpers" sub-menu. You should get something like this.
Click the "Add..." button.
Enter a description, e.g. "Fortran files", and an extension, e.g. .f or .f90.
Enter a MIME type application/octet-stream.
Enter a File type. Four characters exactly are required here. Type e.g. FORT .
Enter a File creator (as for "File type" above).
Make sure the "Plain text" radio button is selected.
Tick "Use for incoming" and "Use for outgoing" check-boxes.
This should look like this. Then click "OK".

Other AD tools:

What are the other Automatic Differentiation tools ? How do they compare to Tapenade ?

This is only our partial vision of the other AD tools. Maybe a better source is the www.autodiff.org site for the Automatic Differentiation community, managed by our colleagues in Aachen and Argonne.

There are AD tools that rely on program overloading rather than program transformation. In general this makes the tool easier to implement. However some overloading-based AD tools can become very sophisticated and efficient, and represent a fair bit of hard work too. Overloading-based AD tools exist only for target languages that permit some form of overloading, e.g. C++ and Fortran95. Overloading-based AD-tools are particularly adapted for differentiations that are mostly local to each statement, i.e. no fancy control flow rescheduling is allowed. On the other hand, these local transformations can be very complex, more than what transformation-based AD tools generally provide. For instance, overloading-based AD-tools can generally compute not only first, but also second, third derivatives and so on, as well as Taylor expansions or interval arithmetic. Adol-C and dco are excellent examples of overloading-based AD tool. Also FADBAD/TADIFF

There are AD tools that transform the original source into a differentiated source. Tapenade is one of those. These tools share their general architecture, with a front-end very much like a compiler, followed with an analysis component, a differentiation component, and finally a back-end that regenerates the differentiated source. They differ in particular in the language that they recognize and differentiate, the AD modes that they provide, and some differences in AD strategies, mostly about the reverse mode. Others transformation-based AD tools are:

Adifor differentiates Fortran77 codes in tangent (direct) mode. Adifor once was extended towards the adjoint (reverse) mode (Adjfor), but we believe this know-how has now been reinjected into the OpenAD framework.
Adic can be seen as the C equivalent of Adifor. However it is based on a completely different architecture, from the OpenAD framework. This framework, very similar to Tapenade's architecture, claims that only front-end and back-end should depend on the particular language, whereas the analysis and differentiation part should work on a language-independent program representation. Adic differentiates ANSI C programs in tangent mode, with the possibility to obtain second derivatives.
OpenAD/F differentiates Fortran codes in tangent and adjoint modes. Its strategy to restore intermediate values in reverse AD is extremely close to Tapenade's. OpenAD/F is made of Adifor and Adjfor components integrated into the OpenAD framework.
TAMC, and its commercial offspring TAF differentiate Fortran files. Taf also differentiates Fortran95 files, under certain restrictions. TAF is commercialized by the FastOpt company in Hamburg, Germany. TAF differentiates in tangent and reverse mode, with the recompute-all approach to restore intermediate values in reverse AD. Checkpointing and an algorithm to avoid useless recomputations (ERA) are used to avoid explosion of run-time. TAF also provides a mode that efficiently computes the sparsity pattern of Jacobian matrices, using bitsets.
TAC++ is the C version of TAF. It is also developped by FastOpt. Presently, TAC++ only handles a large subset of C, and it is still in its development phase, although making significant progress. Like TAF, it will provide tangent and adjoint modes, with the same strategies, e.g. the recompute-all approach with checkpointing for the reverse mode.

There are AD tools that directly interface to an existing compiler. In fact, these are extensions to the compiler so that differentiated code is added at compile time. For instance the NAGWare Fortran95 compiler has AD facilities inside, that are triggered by user directives in the Fortran source. It so far provides tangent-mode differentiation.

There are AD tools that target higher-level languages, such as MATLAB. We know of ADiMat, MAD, and INTLAB. Even when they rely on operator overloading, they may embed a fair bit of program analysis to produce efficient differentiated code.

Directory separator linux/windows:

I need to use "\" as a separator in my paths, and Tapenade uses the UNIX "/" separator.

This happens when your files are stored in a WINDOWS (DOS) file system and you refer to them from a linux system such as cygwin. Use the "-parserfileseparator" option on the Tapenade command line to modify the path separator. For instance:


tapenade ... -parserfileseparator "\" ...


tapenade ... -parserfileseparator "/" ...

JAVA errors: NullPointerException, ArrayOutOfBoundsException, etc:

What does it mean when I get
System: java.lang.NullPointerException
as a message, or similarly an ArrayOutOfBoundsException

It just means you ran into one of the remaining bugs in Tapenade. Please send us a bug report, and we will fix it.

As mentioned in the bug report FAQ section, there is some data that we need in order to track the bug efficiently. If the bug results in a Java exception, such as "java.lang.NullPointerException", then we need the Java execution stack at the time of the crash. To this end, you need to add to your tapenade command the command-line option (where nn is any positive integer number):
-msglevel nn
This forces Tapenade to print the execution stack before crashing. Please send us the exact differentiation command that you typed with all its command-line arguments, and the log text that Tapenade produced before it crashes (including the final execution stack!).

Differentiating multiple top/head procedures, Differentiating Libraries:

I want to differentiate many top/head procedures
I want to differentiate a top/headprocedure for different activity contexts
I want to force the activity context of a given procedure to something larger than Tapenade's choice
I want to differentiate every entry of a library

The recent versions of Tapenade allow you to differentiate several top/head procedures at the same time. We shall call them "heads". Each head may be specified with a particular list of independent input variables and dependent output variables, thus requiring only for the derivatives of the dependent with respect to the independent. See Independent and Dependent sets. This is expressed using the command-line option -head. For instance:

-head "foo(y1 y3)/(x1 x2 x4)" -head "bar(u)/()"

or alternatively

-head "foo(y1 y3)/(x1 x2 x4)  bar(u)/()"

declare two heads, foo and bar. For foo we require differentiation of y1, y3 only, with respect to x1, x2, x4 only. For bar we require differentiation of u only, with respect to all inputs of bar. By default, all inputs are taken as independent, all outputs are taken as dependent.

The alternative equivalent notations -head "foo(x1 x2 x4)\(y1 y3) and -head "foo(x1 x2 x4)>(y1 y3) may be pleasant for people who think of inputs first.

It may happen that Tapenade takes the liberty of adding or removing some variables from the independent and dependent sets. The reasons for doing so are explained in detail here. This behavior may be disturbing, and can be deactivated via the command-line option -fixinterface. This is useful when feeding programs produced by Tapenade into optimization platforms that require a fixed interface.

Function names may be prefixed with their container module (or container procedure) name, as in -head "mod.foo". If no module name is given, Tapenade will look for the procedure outside of any module, then will seach inside modules.

Similarly, variable names are searched in the context of the root procedure given. To disambiguate between global variables from different imported modules, one may prefix the variable name with the module name, as in -head "bar(u mod.glob)/()".

One may also specify only a part of a structured-type variable in the independent and dependent sets. For instance in -head "bar(u.field_a mod.glob)/(v.field_b)".

The disambiguation separator for procedure and variable names may be a dot like in the above examples, or a %

If no differentiation head at all is given, Tapenade will choose one at random, preferring the procedure with the largest call graph below it. A message will be issued about that choice.

By default, when two heads call the same internal procedure, the internal procedure is differentiated only once, with an activity context which is the union of the contexts coming from each head procedure. This is called "generalization". Thanks to the work of Jan Hueckelheim (currently with Queen Mary University of London), Tapenade now has the symmetric behavior called "specialization", where a procedure (whether head or not) may be differentiated several times, once per activity context. This may bring more efficiency at the cost of a larger code. By default, Tapenade applies generalization, but provides options that trigger specialization.

First, one may call for specialization from the command-line, by specifying the same head several times, with different independent and dependent sets as in

-head "foo(y1 y3)/(x1 x2 x4)" -head "foo[V2]()/(x1)"

This will produce two differentiated versions of foo. Please note the extra [V2], used to distinguish the names of the two differentiated procedures. One will be called e.g. foo_d, the other will be called foo_dV2. If the command line does not provide thes disambiguating suffixes, Tapenade will create some arbitrarily (integers from 0 up). One may also ask for specialization of a given subroutine. This is done by placing a directive (aka "pragma") in the source file, just before the header of the subroutine (See details on the location of AD directives. Directive $AD SPECIALIZEACTIVITY placed before a call to some subroutine foo will create a specialized differentiated version of foo for this particular activity call context, except if it is the same as the generalized one. Directive $AD SPECIALIZEACTIVITY placed before the header of foo will trigger specialization at each call site of foo: there will be as many specialized differentiated versions of foo are there are different activity call contexts. Alternatively, the same result is achieved by using the command line option -specializeActivity "foo". Unless they have a special disambiguating suffix defined in the -head command line option, specialized differentiated procedures receive an extra disambiguating suffix, which is an integer from 0 up.

Download Tapenade

Where can I download a local version of Tapenade?

You may download the latest version of Tapenade on your local system from Tapenade download page.

Old versions of Tapenade

How can I get a previous version of Tapenade?

Well, to put it bluntly, you can't !

Sorry but keeping several versions available is a lot of work. More importantly, it contradicts our belief (hope, dream, ?) that successive versions of Tapenade only add new functionalities, improve existing ones, and fix bugs. In the vast majority of cases, this is justified.

However, it did happen in the past that switching to a new version posed a problem to a user. For instance when we introduced the PUSHCONTROL() in version 3.5, or the automatic modification of the user-provided independent and dependent sets in version 2.2. In these cases, the problems could be solved by a small change in the end-user's environment, or a new command-line option. We think it was for the better.

So if you find yourself in this situation, we encourage you to analyze the problem and tell us which is the difference in the differentiated program that poses a problem. A small standalone source file would be great. Hopefully we can find a way so that you can use the new Tapenade and benefit from next improvements.

System errors of the "not found" sort:

Something went wrong after installation: I get a
Exception in thread "main" java.lang.NoClassDefFoundError: toplevel.Tapenade,
Error: Could not find or load main class topLevel.Tapenade
or a message
Tool: Parser not found

Check your environment variable (e.g. shell variable) TAPENADE_HOME.
This variable is used in file bin/tapenade (for the "LINUX" case) and in file bin/tapenade.bat (for the "WINDOWS" case).
Also when switching to a new version of Tapenade, don't forget to update your TAPENADE_HOME variable to refer to the new version, e.g.
TAPENADE_HOME="install_dir"/tapenade3.16
See README.html for more details.

System errors of the "out of memory" sort:

I get a
Exception in thread "main" java.lang.OutOfMemoryError
The Tapenade server complains my source file is too large!

You are probably differentiating a large program!

The Tapenade server will reject your files if the total size of files submitted is over 300000 characters, as many users can access the server simultaneously and too large files make is swap and slow down, or even crash. If you run into this limit, you must probably download a Tapenade executable on your local system.

By the way, it still happens that the server crashes because of too many users differentiating too large files. In this case the server should restart automatically, so please wait for a moment and retry.

For a locally installed Tapenade, if the java heap overflows (java.lang.OutOfMemoryError), increase the heap size from the command-line by specifying java options such as:


tapenade -java "-Xmx2048m"

With older versions of Tapenade and windows versions, increase the heap size in the launching script file bin/tapenade (for the "LINUX" case) or in file bin/tapenade.bat (for the "WINDOWS" case).
Set HEAP_SIZE=-mx2048m or even HEAP_SIZE=-mx4096m

Sending remarks, questions, and bug reports:

Where should I submit questions about Tapenade ?
How do I send bug reports to the Tapenade development team ?

First of all, this is a very good idea. Thanks !
Bug reports should be sent to the developers of Tapenade at this e-mail address: tapenade@inria.fr Mail to ...

On the other hand, questions and remarks should rather be sent to the tapenade-users mailing list. You will have to subscribe

first, then you will be able to submit your questions and remarks by mailing to tapenade-users@inria.fr. Maybe some other user of Tapenade will answer even before we do! Naturally, frequently asked questions should eventually be included here.

If you really don't want to subscribe, then you may just send an e-mail to the developers of Tapenade Mail to ...

More specifically about bugs, there is some data that we need in order to track the bug efficiently. If the bug results in a Java exception, such as "java.lang.NullPointerException", then we need the Java execution stack at the time of the crash. To this end, you need to add to your tapenade command the command-line option (where nn is any positive integer number):
-msglevel nn
This forces Tapenade to print the execution stack before crashing. Please send us the exact differentiation command that you typed with all its command-line arguments, and the log text that Tapenade produced before it crashes (including the final execution stack!).

If you can send us (a reduced version of) the file that causes the bug, that would be just great!

If you were using the on-line Tapenade, then you got an "Error" web page. At the end is a useful link (for us developpers): "If everything seems correct, it is probably an internal bug. In that case, please send us this bug report, without modifying the contents of the message. We will examine it promptly.". Please send us this bug report using the button "send us". It will send us the session reference so that we can find its track in our very large local log. Most important for that are the session number and the date/time of the session, for example: Session:ac3eQiTVfzwb, Time:Wed Mar 29 07:59:01 MEST 2006

JAVA Version required:

I installed the new version of Tapenade and Java now complains.
I am getting a runtime exception UnsupportedClassVersionError
What minimal version of Java jdk is required?

A locally installed version of Tapenade requires that your installed version of Java is up to date. For instance, as of march 2015, we compile Tapenade with Java jdk 1.8.

It may happen that older Java versions accept the compiled Tapenade that we provide, but we cannot guarantee it. If they don't, you will get a Java error/exception right away, about class versions incompatibility.

Wrong external's:

My differentiated program does not compile because it contains a
external REAL
declaration.

Tapenade doesn't well recognize the REAL Fortran intrinsic, and therefore considers it as an external. This may also happen for a couple others intrinsics. This bug has still not been fixed. The workaround is simple: just delete the faulty declaration.

Placement of `$AD` directives:

The directives that I inserted into my source don't work.
Tapenade doesn't recognize my $AD directives.
What it the correct placement/location of $AD directives?

Tapenade directives (i.e. of the form $AD xxx) cannot be placed anywhere in the source. If they are misplaced, chances are that Tapenade will just ignore them.

Directives that (may) concern a whole procedure can be attached to the procedure header, i.e. placed on a new line which is immediately before the procedure header. There may be comments between the directive line and the procedure header, but there must be no code.

Directives that (may) concern a single instruction can be attached to the instruction, i.e. placed on a new line which is immediately before the instruction. Beware that "syntactic sugar", such as else, endif, enddo, end, opening or closing brace { ... }, or (for most directives) declaration statements, are not instructions. Syntactic sugar is eliminated by Tapenade at parsing, and their attached directives are eliminated too. There may be comments between the directive line and the instruction, but there must be no code.

Some directives work by pairs, because they actually apply to portions of code, so there must be two directives that designate the "start" and the "end" of the portion. Designating a portion of code P makes sense only when P could indeed be extracted as a separate procedure.

The "start" directive must be placed immediately before the first statement that is in P.
The "end" directive must be placed immediately before the first statement out of P, i.e. the first statement that follows the end of P.

These "first statement in" and "first statement out" must be unambiguous. All predecessors of the "first statement in" must be out of P. All predecessors of the "first statement out" must be in P. If necessary, introduce a no-op statement (e.g. continue) to lift ambiguities. There must be no entry into P that does not go through the "first statement in", and no exit from P that does not go through the "first statement out". Finally, "first statement in" and "first statement out" must be executable statements, not declaration statements nor pure control (e.g. closing braces, else, end...).

If you feel that must attach a directive at some location and there is no instruction there to attach it to, insert a no-op instruction such as continue and attach the directive to it. For instance if your source is:


      IF (x>0) THEN
        y = foo(x)
        x = x*y
      ELSE
        x = 0.0
      ENDIF
      z = 2*x

and you want to trigger a "checkpoint" on the "then" branch (see User-defined additional checkpoints ...) then you are in trouble to designate the end of the "then" branch because there is no statement there: the else is not an instruction, the x = 0.0 is certainly not the end of the "then" branch, and nor is the z = 2*x. The solution is to modify your source as follows:


      IF (x>0) THEN
C$AD CHECKPOINT-START
        y = foo(x)
        x = x*y
C$AD CHECKPOINT-END
        CONTINUE
      ELSE
        x = 0.0
      ENDIF
      z = 2*x

Controlling checkpointing in the reverse mode (`$AD NOCHECKPOINT`):

My reverse-differentiated program is too slow, and I think it comes from checkpointing.
How can I tell Tapenade to refrain from checkpointing each and every procedure call ? How can I tell Tapenade to use checkpointing on a given piece of code ?

By default, Tapenade will apply checkpointing to each and every procedure call, i.e. subroutine or function call. There are various directives that let the user control checkpointing. When used wisely, these techniques can vastly improve the performance of the adjoint differentiated code by modifying the tradeoff between memory use and extra recomputing.

There are three ways to specify places (i.e. procedure calls) where checkpointing must not be done.

You can place a $AD NOCHECKPOINT directive in the source just before a particular procedure call. For example (here with F77 syntax for comments. i.e. a "C" in column 1):
```
C$AD NOCHECKPOINT
      w = toto(x, y, z)
```
tells Tapenade not to place a checkpoint around this particular call to function toto.
You can place a directive in the source just before the definition of a procedure. For example:
```
C$AD NOCHECKPOINT
       subroutine titi(a,b)
```
tells Tapenade not to place a checkpoint around any call to subroutine titi.
You can use the command-line argument -nocheckpoint that takes the list of procedures that must never be checkpointed. For example:
```
   $> tapenade -b -nocheckpoint "toto titi" program.f
```
will checkpoint no call to subroutines toto and titi.

Conversely you can ask Tapenade to apply checkpointing on an arbitrary piece of code.

You can place the pairs of directives described here.
Another way, with more effort but that gives you more control, is to make this piece of code a true subroutine: since Tapenade applies checkpointing systematically to each subroutine call, you will obtain the desired effect.

Finally there are situations where you can use special predefined checkpointing strategies:

loops with independent iterations, and in particular parallel or parallelizable loops,
fixed-point loops, often used to solve implicit functions,
binomial checkpointing, which applies well to long chains of similar iterations such as time-stepping loops.

Independent Iterations Loops (`$AD II-LOOP`):

What is the $AD II-LOOP directive? When can I use it ?

The II-LOOP directive ($AD II-LOOP) tells Tapenade that the following loop has "Independent Iterations", i.e. roughly speaking can be parallelized. With this information, Tapenade is able to produce a better code in the reverse mode.

A loop can be declared II-LOOP if it has no loop-carried "true" or "flow" data-dependence, i.e. if no loop iteration depends on a value that is computed by another iteration. The following loop is an II-LOOP (here with F77 syntax for comments. i.e. a "C" in column 1):


C$AD II-LOOP
        DO i=1,N,2
          A(i) = 2.0*z
          A(i+1) = 3.0*z
          tmp1 = B(T(i))
          tmp2 = B(K(i))
          vv = SQRT(tmp1*tmp2)
          C(i) = C(i)+vv
        ENDDO

because, as you can check, there is no loop-carried true dependence. This implies that the iteration order can be freely shuffled. On the other hand, the following loop is not an II-LOOP:


        DO i=3,N-2
          A(i) = A(i-2)
          B(i) = B(i+2)
          prod = prod*C(i)
        ENDDO

for at least three reasons:

There is a loop-carried flow dependence of distance 2 on A
There is a loop-carried anti dependence of distance 2 on B, and it will become a flow dependence if the iteration order is reversed.
There is a loop carried dependence on the product prod

Finally, the following is also an II-LOOP:


C$AD II-LOOP
        DO i=1,N,2
          tmp1 = B(T(i))
          tmp2 = B(K(i))
          vv = SQRT(tmp1*tmp2)
          sum = sum+vv
        ENDDO

Because the loop carried dependence on sum indeed comes from a "sum" reduction, which is OK.

If you add the directive $AD II-LOOP as a comment just before an II-LOOP, you will see that reverse differentiation will produce a different code, which uses significantly less PUSH/POP memory space ("tape") than without the directive.
More explanations in the paper on Adjoining Independent Computations

Fixed-Point Loops (`$AD FP-LOOP`):

What is the $AD FP-LOOP directive? When can I use it ?
My code uses a fixed-point iterative loop, and its adjoint uses too much memory
My code uses a Newton iteration, and I want to take advantage of this for its adjoint

The FP-LOOP directive ($AD FP-LOOP) tells Tapenade that the designated loop is actually a fixed-point iteration that is: it repeatedly runs the assignment


   Z = PHI(Z,X)

until Z becomes ``sufficiently'' stationnary. There are other assumptions/restrictions such that X is never modified in this loop. As a result, the final, stationnary value of Z is in fact a function of (only) X, regardless of the initial value of Z. In other words, Z is defined implicitly as the solution of PHI(Z,X)-Z = 0.

There are special strategies for an efficient adjoint of these fixed-point loops. We selected the strategy proposed by Bruce Christianson (Reverse accumulation and implicit functions, Optimization Methods and Software , vol 9 , no. 4 , pp. 307-322, 1998), which seems better adapted to our adjoint AD model. The main advantage of this strategy is that intermediate values computed during evaluation of PHI(Z,X) are stored only for the last, converged iteration. Another advantage is that when convergence is equal to or better than quadratic (e.g. for Newton iterations), the adjoint loop will iterate only once to reach convergence.

Tapenade is now able to produce an adjoint code that applies this strategy automatically, triggered by the FP-LOOP directive ($AD FP-LOOP). Consider this code snippet (here with F77 syntax for comments. i.e. a "C" in column 1):


      ...
      z = 0.5
      oz = z+1
C$AD FP-LOOP "z"
      DO WHILE ((z-oz)**2 .GE. 1.e-10)
         oz = z
         IF (z.lt.0.0) THEN
            z = -z*z
         ELSE
            z = z*z
         ENDIF
         z = sin(z*x)
      ENDDO
      foo = 3*z
      ...

This is a (very simple) fixed-point loop. We assume that it converges. The directive tells Tapenade that the state, i.e. the variables that eventually becomes stationnary, is here the single variable z. The parameters, found automatically by static data-flow analysis, are here the single variable x. In adjoint mode, Tapenade will generate code that implements Christianson's efficient strategy.

You can tune the convergence criterion of the adjoint fixed-point iteration by adding info into the FP-LOOP directive. Starting from the above example, writing:


C$AD FP-LOOP "z" adj_residual=5.e-5

will make the adjoint fixed-point stop as soon as the residual (here (z_n - z_(n-1))^2) goes below 5.e-5. Alternatively, writing:


C$AD FP-LOOP "z" adj_reduction=2.e-6

will make the adjoint fixed-point stop as soon as the ratio between the initial residual (here (z_1 - z_0)^2) and the current residual ((z_n - z_(n-1))^2) goes below 2.e-6.
Note: the parser for directives is rudimentary: don't write any white space inside the directive parts adj_residual=5.e-5 or adj_reduction=2.e-6.

To be executed, the differentiated code must be linked with the definitions of one or both of the external routines:

adFixedPoint_tooLarge()
adFixedPoint_notReduced()

User-defined additional checkpoints (`$AD CHECKPOINT-START` and `$AD CHECKPOINT-END`):

How can I add reverse-mode checkpoints into my source code?
How can I force checkpointing of a given piece of code?

Just place Tapenade directives $AD CHECKPOINT-START and $AD CHECKPOINT-END around the piece of code you want to checkpoint. This allows you to define a checkpoint around a piece of code P. This may prove useful in very long subroutines, that consume a lot of memory to store their intermediate variables during the forward sweep.

Adding a user-defined checkpoint around a piece of code P is applicable when P could indeed be extracted as a separate procedure. In the previous versions of Tapenade, you had to actually make P a procedure to trigger checkpointing on it. These directives achieve the same effect without forcing you to make this error-prone transformation.

The $AD CHECKPOINT-START must be placed immediately before the first statement that is in P.
The $AD CHECKPOINT-END must be placed immediately before the first statement out of P, i.e. the first statement that follows the end of P.

Make sure these "first statement in" and "first statement out" are unambiguous. All predecessors of the "first statement in" must be out of P. All predecessors of the "first statement out" must be in P. If necessary, introduce a no-op statement (e.g. CONTINUE) to lift ambiguities. There must be no entry into P that does not go through the "first statement in", and no exit from P that does not go through the "first statement out". Finally, "first statement in" and "first statement out" must be executable statements, not declaration statements nor pure control (e.g. closing braces, ELSE, END, ...) User-defined checkpoints can be nested. The following piece of code gives an example (here with F77 syntax for comments. i.e. a "C" in column 1):


      if (x.gt.10.0) then
C$AD CHECKPOINT-START
         x = x*y
         if (x.gt.0.0) x =-x
C$AD CHECKPOINT-START
         y = y - x*x
         y = y*y
C$AD CHECKPOINT-END
         x = x + sin(y)
C$AD CHECKPOINT-END
         continue
         ...
      endif

It contains two nested checkpoints, both located inside the "true" branch of a conditional. The generated code shows the effect of these additional checkpoints. In the forward sweep:


      IF (x .GT. 10.0) THEN
        CALL PUSHREAL4(x)
        CALL PUSHREAL4(y)
        x = x*y
        IF (x .GT. 0.0) x = -x
        y = y - x*x
        y = y*y
        x = x + SIN(y)
        ...
        CALL PUSHCONTROL1B(1)
      ELSE
        CALL PUSHCONTROL1B(0)
      END IF

and in the reverse sweep:


      CALL POPCONTROL1B(branch)
      IF (branch .NE. 0) THEN
        ...
        CALL POPREAL4(y)
        CALL POPREAL4(x)
        CALL PUSHREAL4(x)
        x = x*y
        IF (x .GT. 0.0) THEN
          x = -x
          CALL PUSHCONTROL1B(1)
        ELSE
          CALL PUSHCONTROL1B(0)
        END IF
        CALL PUSHREAL4(y)
        y = y - x*x
        y = y*y
        yb = yb + COS(y)*xb
        CALL LOOKREAL4(y)
        y = y - x*x
        yb = 2*y*yb
        xb = xb - 2*x*yb
        CALL POPREAL4(y)
        CALL POPCONTROL1B(branch)
        IF (branch .NE. 0) xb = -xb
        CALL POPREAL4(x)
        yb = yb + x*xb
        xb = y*xb
      END IF

User-defined fragments not-to-differentiate (`$AD DO-NOT-DIFF` and `$AD END-DO-NOT-DIFF`):

I can write a much better differentiated code by hand !
How can tell Tapenade to let me differentiate some fragment myself ?

Place directives $AD DO-NOT-DIFF and $AD END-DO-NOT-DIFF around the piece of source code that you don't want Tapenade to differentiate. Tapenade will not differentiate the code fragment between these directives, and will leave a "hole" in the differentiated code, which you can locate by searching for markers $AD DID-NOT-DIFF and $AD END-DID-NOT-DIFF. It is up to you to provide the correct differentiated code between these markers.

In tangent mode, the "hole" will consist only of the source code of the fragment. In adjoint mode, the "hole" will just be empty.

Please note that Tapenade will still run all data-flow analyses on the complete code, including the "DO-NOT-DIFF" fragments. This implies that differentiation will still make the same choices for the rest of the code, whether there are "DO-NOT-DIFF" fragments or not.

Directives $AD DO-NOT-DIFF and $AD END-DO-NOT-DIFF are both followed by an optional label, that Tapenade uses to check matching directives, and that you will use to distinguish between several "not-to-differentiate" fragments in the differentiated code.

Directives $AD DO-NOT-DIFF and $AD END-DO-NOT-DIFF are seen as "attached" to the statement that follows them. This statement that follows must be a true statement and not some syntactic sugar such as end, end if, else, enddo... If this is not the case, you may have to insert a a no-op statement (e.g. CONTINUE), which is a "true" (although empty) statement. Also, like required for $AD DO-NOT-DIFF and $AD END-DO-NOT-DIFF, there must be no entry into the fragment that does not enter through its "first statement in", and no exit from the fragment that does not go through the "first statement out". All predecessors of the "first statement in" must be out of the fragment. All predecessors of the "first statement out" must be in the fragment. (see User-defined additional checkpoints).

Binomial Checkpointing (`$AD BINOMIAL-CKP`):

My time-stepping loop fills up the memory space during the forward sweep, and this makes my adjoint code crash.
What is the $AD BINOMIAL-CKP directive? When can I use it ?

Binomial checkpointing is the optimal memory/runtime tradeoff for iterative loops, i.e. loops where the computation of iteration n depends on the results of previous iterations, and therefore there is no hope of making these iterations independent and/or run them in parallel. A typical example is the time-stepping loop in an instationnary simulation.

Assuming that the final number of iterations N is known, and assuming that each iteration has the same runtime cost, then A. Griewank has given a checkpointing strategy for the iterative loop, which is optimal both in terms of memory used to store the checkpoints, and in terms of runtime i.e. the number of times a given iteration is repeated. A.Griewank has shown that this so-called "binomial" strategy has a cost in memory and a cost in execution time that grow like log(N). More precisely

The maximum number of checkpoint snapshots (i.e. bunches of values required to restart execution from a given iteration) present in memory at the same time grows like log(N). Therefore the maximum memory required is log(N) times the size of one snapshot.
The maximum number of times a given iteration with be repeatedly executed due to this strategy also grows like log(N). Therefore the time required to compute the adjoint of the N iterations will be (log(N) + Constant) times longer than the time to run the original N iterations.

In practice, one has less flexibility on the number of snapshots than on the runtime. Therefore one prefers to fix the maximum number of snapshots to a fixed q. Then the costs of the binomial scheme change to:

The maximum memory required is q times the size of one snapshot. It is independent of N.
The time required to compute the adjoint of the N iterations will grow like the q-th root of N.

This was published by A. Griewank and A. Walther, and first implemented in AdolC. Tapenade is now able to produce an adjoint code that applies this strategy automatically, triggered by the BINOMIAL-CKP directive ($AD BINOMIAL-CKP). Consider this example (here with F77 syntax for comments. i.e. a "C" in column 1):


C$AD BINOMIAL-CKP nstp-stp1+2 4 stp1
      do stp=stp1,nstp
         x = x+y
         y = y-x*x
         v3 = 1.0
         do i=3,98
            j = i-stp/10
            v1 = A(j)*B(i)
            v2 = B(j)/A(i+1)+v3
            A(i) = 2*A(i)+sin(C(j))
            B(i-1) = B(i)*B(i+2) - A(i+1)*A(i-1)
            A(i+1) = A(i)+v1*v2
            B(i-1) = B(i)+v2*v3
            v3 = v3+v2-v1
         enddo
         A(j) = A(i)*B(j)
      enddo

The outer loop is a good candidate for binomial checkpointing. Its iterations are definitely not independent, so the II-LOOP directive is out of question. Also, the number of iterations, although dynamic, is known before the loop starts.

The inner loop could also be applied binomial checkpointing, but this would be less profitable as it is a smaller piece of code. The three values provided after the BINOMIAL-CKP directive are

The number of iteration steps, or an expression to compute it just before the loop starts. For optimal results, also count the iteration during which loop exit occurs. This is why we wrote nstp-stp1+2 instead of nstp-stp1+1. If the given number of iterations is wrong, the differentiated code should still work, but will be less efficient in time or memory.
The maximum number q of allowed snapshots, chosen by the end-user
The index of the first step in the sequence

Warning: as Tapenade parser is not perfect inside directives, be careful not to put any white space inside these three expressions. These expressions will we copied verbatim in the adjoint code.

If you look at the produced reverse code, you will find that the adjoint code is in fact a driver, initialized with the parameters of the BINOMIAL-CKP directive, and that will trigger the correct sequence of actions to compute the adjoint of the iterative loop. These actions are:

Push Snapshot: Push the current memory state on the stack.
Look Snapshot: Restore the memory state from the stack, but leave it on the stack.
Pop Snapshot: Restore the memory state from the stack and remove it from the stack
Advance: run the next iteration in its original form, without any derivative computed nor value pushed.
First Turn: Compute the adjoint of the last iteration and of the rest of the code.
Turn: Compute the adjoint of an ordinary iteration (not the last one)

To be executed, the differentiated code must be linked with the definitions of the external routines used by the driver:

TRV_INIT()
TRV_NEXT_ACTION()
TRV_RESIZE()

Linear Solvers:

My original code solves a linear system and the differentiated code for this part of the code is slow.
My original code uses an iterative linear solver and the differentiated code produces derivatives whose accuracy gets poorer and poorer as the differentiated linear solver is used.

Linear solvers are often sophisticated and do not lend themselves to Automatic Differentiation efficiently. Even if you have access to the source of the linear solver, it may be wiser not to use the AD-generated code for this solver, and write a better one by hand.

Moreover, when the linear solver is iterative, it often happens that the number of iterations required to fully converge the solution y of Ay = b is not enough to converge its derivative yd or yb. Since AD uses the same control as the original program, it stops iteration when the original program does. Therefore yd or yb may not have reached convergence when y has!

Of course if you use a solver from a library and you don't have access to the source, then you are forced to write the differentiated solver by hand. You have no choice. It will just comfort you to learn that this is the best thing to do anyway! Just refer to the FAQ item about Black-box procedures to tell Tapenade about this library call (We would advise you to apply the dummy procedure method), and come back here for hints about how to write this hand-coded differentiated linear solver.

Assume that the code to be differentiated has first built a matrix A and a right-hand side vector b, that may be both active. Size of A is n*n and size of b is n. Assume that some solver is called, e.g.


        call SOLVE(A,y,b,n)

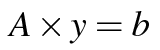
that computes the y (of size n) such that:

y is also active. In tangent mode, we can differentiate the above equation by hand and we obtain:

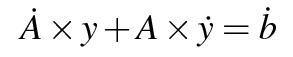
so that we find yd is:

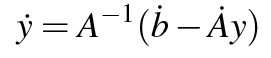
Therefore, since Tapenade probably built a tangent differentiated call looking like:


        call SOLVE_D(A,Ad,y,yd,b,bd,n)

you can write your hand-coded SOLVE_D along the lines of:


        subroutine SOLVE_D(A,Ad,y,yd,b,bd,n)
        INTEGER n
        REAL A(n,n), Ad(n,n)
        REAL y(n), yd(n), b(n), bd(n)
        INTEGER i,j
        REAL RHSd(n)

        call SOLVE(A,y,b,n)
        DO i=1,n
          RHSd(i) = bd(i)
          DO j=1,n
            RHSd(i) = RHSd(i) - Ad(i,j)*y(j)
          ENDDO
        ENDDO
        call SOLVE(A,Yd,RHSd,n)
        END

In reverse mode, it's no surprise things get a little harder! The inputs of the linear solver call are A and b, and the output is y. By definition of the adjoint variables Ab, bb, and yb, we have the dot products equality (dot product noted as (_|_)) for any Ad and bd :

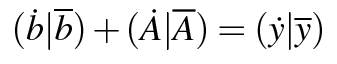
Beware that these dot products are element-wise: the dot product of Ad and Ab is the sum of all Ad(i,j)*Ab(i,j) for all i and j. Replacing yd by its above definition, we get:

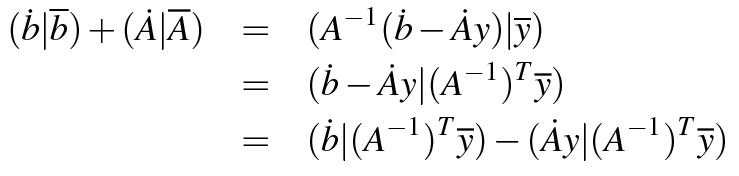
for any Ad and bd. Therefore:

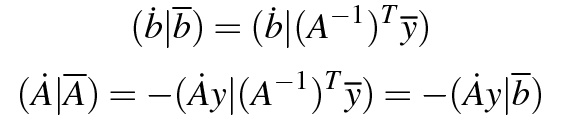
The first equation gives directly bb as:

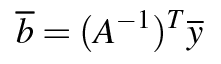
The second equation gives Ab but this is less obvious: we must go down to the indices level:

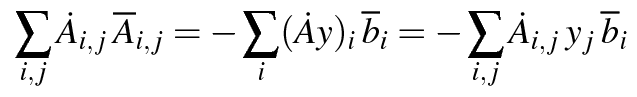
and we get the value of each element of Ab:

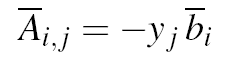
which is the (opposite) outer product of y and bb.

Finally, let's not forget that the original solver overwrites y with the solution, which implies that the adjoint solver must reset yb to zero before returning.

Since Tapenade probably built a reverse differentiated call looking like:


        call SOLVE_B(A,Ab,y,yb,b,bb,n)

you can write your hand-coded SOLVE_B along the lines of:


        subroutine SOLVE_B(A,Ab,y,yb,b,bb,n)
        INTEGER n
        REAL A(n,n), Ab(n,n)
        REAL y(n), yb(n), b(n), bb(n)
        INTEGER i,j
        REAL AT(n,n), incrbb(n)

        DO i=1,n
          DO j=1,n
            AT(i,j) = A(j,i)
          ENDDO
        ENDDO
        call SOLVE(AT, incrbb, yb, n)
        DO j=1,n
          bb(j) = bb(j) + incrbb(j)
        ENDDO
        call SOLVE(A,y,b,n)
        DO i=1,n
          DO j=1,n
            Ab(i,j) = Ab(i,j) - y(j)*incrbb(i)
          ENDDO
          yb(i) = 0.0
        ENDDO
        END

Two remarks:

first, notice that this code increments Ab and bb instead of just setting them. This is the usual adjoint behavior that comes from the fact that A and b may very well be used elsewhere in the program and therefore may have other influences on the dependent outputs.
Second, we have been considering in these examples that both A and b are active. If either one is not active, then the codes above may be simplified.

Multiple sessions in parallel:

The differentiated code contains parts that do not correspond to anything in my original code.

Maybe you have two web Tapenade sessions active at the same time. When using the Tapenade server on the web, there can be only one differentiation page opened at a time. Do not try to open two different web browser pages, and call one Tapenade in each, because your Tapenade session is unique: therefore the files you upload would all go into the same directory here, causing strange behavior.

Approximative source-code correspondence:

You claim that the graphical interface shows the correspondence between source and differentiated code. I can't see it!

This source-code correspondence is implemented through html links and anchors, so its behavior is approximate. All it guarantees is that the target of the link is somewhere visible on the page, but not necessarily in front of the source.

Moreover there are situations where source-code correspondence is lost, for example on declarations. So in this case, the best target we can show is the enclosing generated subroutine.

Too many Warning and Error messages:

Help! Tapenade sends me plenty of error messages !

Yes Tapenade sends plenty of error messages! One may think there are too many of them. This is because we believe these messages can be very helpful in the case when you obtain wrong differentiated values. Sometimes one of these messages is an indication of a real problem for differentiation, so it can save you a lot of time to look at them.

However, maybe you should not try too hard to get rid of all these messages. After all many of them are purely warnings. Very often, Tapenade will produce a correct differentiated code, even if it has complained. We strongly advise you to look at the detailed discussion on messages which indicates, for each message, whether it is really important (or not), and why, especially from the AD point of view.

Tapenade lets you define in the command line an error level threshold, below which errors are not shown any more.

Finally, to summarize, please do not overlook Tapenade errors because they potentially indicate hard differentiation problems, and at the same time do not be too demanding on the source program: some warnings are there to stay!

Includes and Comments:

What a mess! the nice include files of my original program have all been expanded in the differentiated program !
What a mess! all my nice comments around declarations have been displaced or lost !

This still happens for some programs. Sorry about that.

For a very long time, you can understand this has not been our topmost priority. After all, it was more urgent to make differentiated programs that run, right?

Also this was not so easy because the internal representation of Tapenade used to digest every declaration into symbol tables that did not remember where declarations came from. For the same reason, we had nowhere to keep comments attached to declarations. This has been improved for version 3. So hopefully, you should notice an improvement in that respect. Sometimes when the code uses the implicit feature of Fortran77, the include "calls" can't be placed back. Use implicit none to avoid that.

Despite our efforts, it may happen that some comments are lost. This is a bug and we will be grateful if you signal it to us.

Default sizes of basic data types:

My system/compiler has a default size of 8 bytes for REAL, and Tapenade has a default size of 4 bytes.

By default, Tapenade assumes that the actual sizes in memory of basic data types are as follows:
INTEGER: 4 bytes,
REAL: 4 bytes,
DOUBLE PRECISION: 8 bytes,
COMPLEX: 8 bytes,
DOUBLE COMPLEX: 16 bytes,
LOGICAL: 4 byte,
CHARACTER: 1 byte,

These values are important to solve EQUIVALENCEs, or to match different declarations of the same COMMON block, or more importantly for the PUSH/POP mechanism of the reverse mode.

Please check that your system/compiler uses the same sizes. In case of doubt, we provide a small tool to check this. Tapenade lets you declare new default sizes with the following options:
-i2 -i4 -i8 -r4 -r8
other options might be created as necessary...

Parameterized array sizes:

My original file declares array A(N+1), and the code generated by Tapenade declares it as A(201)

This is true, and we understand it makes the new code less easy to maintain. When N is a constant, whose value is known statically, e.g. 200, Tapenade internally solves the N+1 into its value, here 201. This is on our list of things to improve.

Some cases of "segmentation fault":

My differentiated program crashes with a "segmentation fault".

Yes. This may still happen. Sigh...
Here are some (not so frequent) cases, that happen in the reverse mode:

Differentiation raised an AD10 message such as (AD10) Differentiation of procedure FOO needs to save and restore the I-O state. This may mean that FOO only opens or only closes an I-O file. If a call to FOO is checkpointed, this may result in the file being opened or closed twice, and this can cause a run-time error. You can work around this by using a $AD NOCHECKPOINT directive, or by modifying the source code. Keep in mind however that I-O in the differentiated code are almost always a nuisance.
There are not as many PUSH'es and POP's because the control flow is not inversed well. The symptom is that the crash occurs inside a POP, and the stack is empty. If this occurs to you, it is a Tapenade bug. Please signal it to us.
If your program passes a FORTRAN PARAMETER (i.e. a constant) as an argument to another procedure, Tapenade tries to PUSH/POP this constant, which results in a segmentation fault at the POP. Until we fix that, don't pass a PARAMETER as an argument.

Vector (i.e. Multi-directional) modes (i.e. option `-multi` or `-vector`):

What do I do with the code generated with the option -vector?
What is this DIFFSIZES.inc include file used in the differentiated code?
What is this extra dimension in the differentiated variables?
What is the relation between variables nd, nbdirs and nbdirsmax?

The option -multi (or -vector) turns on multi-directional mode, which produces a code that will compute the derivatives at a single point in the input space but

if in tangent mode, along several directions in the input space,
if in adjoint mode, for several weightings in the output space.

The way it works is by modifying the structure of the derivative variables. In standard, single-direction mode, a derivative variable retains the structure of its original variable (except for structures, in which non-active components disappear from the differentiated structure). In multi-directional mode, derivative variables receive one extra dimension, that corresponds to the multiple possible directions (or weightings). For instance a scalar variable


       real*8 xx

will be differentiated if active into:


       real*8 xxd(nbdirsmax)

and an array variable


       real*8 aa(100,N)

will be differentiated if active into:


       real*8 aad(nbdirsmax,100,N)

Notice that the extra dimension is added on the left in FORTRAN, and conversely on the right in C, i.e. in the deepest dimension location. This is useful to isolate the array of derivatives of a given element of aad. Also notice that the (static) size of this new dimension is fixed to nbdirsmax, which must be at least equal to the maximum number of directions you plan to explore at a time.

The differentiated instructions are modified accordingly. A statement such as


       a(i1, i2) = 2*b(i1, i2)

will be differentiated as


       DO nd=1,nbdirs
         ad(nd, i1, i2) = 2*bd(nd, i1, i2)
       ENDDO

Notice that the loop on differentiation directions is placed at the deepest level of the code's loop nesting. Also these loops iterate nbdirs times, thus allowing you to select at run time a number of directions less or equal to nbdirsmax. nd is just the index that spans on the nbdirs directions. When possible, Tapenade tries to merge these loops on dimensions, to reduce loop overhead. Notice finally that there is no such loop around differentiated procedure calls, as the loops on directions will be placed inside the differentiated procedure.

nbdirs is dynamic, so it is an extra parameter to be passed to the differentiated procedures. on the other hand, nbdirsmax is static: you must provide it at compile time. Tapenade strongly suggests that you define it in an include file named DIFFSIZES.inc. Tapenade adds the include command that includes this file. All you have to do is to create this file. In general, you need to do that only once. For instance, this file may contain


       integer nbdirsmax
       parameter (nbdirsmax = 50)

In Fortran90, a module DIFFSIZES is used instead of an include file. You have to write it so that it defines the constant nbdirsmax.

Getting the Jacobian using the Multi-directional mode:

How can I use the Multi-directional mode to compute a Jacobian?

Some easy theory to begin with.
Consider a procedure P(X,Y), that evaluates a math function F: X -> Y. Tangent mode AD of P produces a tangent code P_D(X,XD,Y,YD) that computes and returns:

the same Y = F(X)
and in addition YD = J*XD, where J is the Jacobian of F at point X.

If your goal is to obtain the Jacobian J, and knowing that the tangent code gives you J*XD for any XD, you see that the tangent code will give you any column of J by just providing a XD which is the corresponding vector of the Cartesian basis of the space of X's. In other words, if you provide XD full of 0.0 except for a 1.0 at rank i, then you will obtain a YD = J*XD that is the i-th column of J. If you do this repeatedly, you will get all the columns of J, and therefore J.

So you need nothing more than the plain tangent mode of AD to obtain J. However, you see that this amounts to running P_D several times for different XD's but for the same X. Some identical computations are going to be duplicated. Multi-directional tangent mode just lets you factor out these identical computations: just ask Tapenade to produce the multi-directional tangent code of P, and then run this multi-directional tangent code with an XD which has now an extra dimension (at the deepest level) so that it contains all the vectors of the Cartesian basis of the input space (the space of X's).

Technical details of the multi-directional mode are explained here.

We also have in this FAQ a short discussion about Jacobians and Hessians by AD. Take a look at it, especially in its second part devoted to the Jacobian: it contains further discussion about Jacobian sparsity and the multi directional adjoint/reverse mode.

A final warning about the Jacobian built by multi-directional mode: In multi-directional tangent, all derivative variables receive naturally an extra dimension, which ranges over the different directions of differentiation, i.e. over the dimensions of the input space. For implementation reasons, this extra dimension must be the "deepest" dimension in the new differentiated variable. This is because we must be able to easily extract the derivatives of any element of any array. This has a consequence on the shape of the differentiated output. Suppose that the output Y is actually an array Y(1:10). The derivative result, which you may think of as the Jacobian, will have an extra dimension at the deepest location.

For instance in Fortran, this will be YD(1:nbd,1:10) where nbd is the number of directions, which is (forgetting about sparsity) the dimension of the input space. On the other hand, the second dimension is linked to the dimension of the output space.

You must take this into accout when giving this YD to a procedure that asks for the Jacobian: the conventions on dimensions must match and if they don't you may have to build the transpose of YD or modify the using procedure.

Second Derivatives and Hessians:

Can Tapenade return second derivatives?
Can Tapenade create a file to calculate Hessian also?

Basically yes! However this requires a bit more interaction with the end-user. Also the resulting differentiated programs could be improved further if Tapenade had a special mode for second derivatives. There is some ongoing research on these questions in our research team.

The idea to obtain second derivatives is to apply Automatic Differentiation twice. Starting from a procedure P in file p.f that computes y = f(x), a first run of Tapenade e.g. in tangent mode through the command line:


   $> tapenade -d -head P -vars "x" -outvars "y" p.f

returns in file p_d.f a procedure P_D that computes yd = f'(x).xd. Now a new run of Tapenade on the resulting file e.g. in tangent mode again through the command line:


   $> tapenade -d -head P_D -vars "x" -outvars "yd" p_d.f

returns in file p_d_d.f a procedure P_D_D that computes ydd = f''(x).xd.xd0
Specifically if you call P_D_D with inputs xd=1.0 and xd0=1.0 in addition to the current x, you obtain in output ydd the second derivative f''(x).

TANGENT-ON-TANGENT APPROACH:

In more realistic cases, the input x can be multi-dimensional. The output y can be multi-dimensional too, but this is not so much of a problem here. If you look for the second partial derivative d²y/dx_idx_j, you may apply the same two steps, differentiating P with respect to input x_i first, then differentiating the resulting P_D with respect to input x_j. If in reality x_i or x_j are indeed elements of a larger variable, e.g. elements of an array x, you must differentiate with respect to the larger variable. This is because Tapenade does not let you differentiate with respect to individual array elements. Then if you call the resulting procedure P_D_D with "correct" inputs xd and xd0, you obtain the second derivative(s) that you want in output ydd. Finally what are the "correct" values to initialize xd and xd0? In the special case of simple scalars, it is just 1.0. In the general case of array elements, set arrays xd and xd0 to 0.0, except for elements xd(i) and xd0(j) which must be set to 1.0.

Going one step further, one may want several such derivatives d²y/dx_idx_j for a bunch of x_i or x_j. The natural answer is then to use tapenade multi-directional mode to compute all these derivatives in just one run. This works fine when multi-directional mode is called for only one of the two steps. In other words, what you get then is either a row or a column of the complete Hessian matrix. In the general case where one wants to compute the complete Hessian, one needs to call both differentiations in multi-directional mode. Doing this, you might encouter a couple of simple problems that you will need to fix by hand like we usually do:

The first multi-directional differentiation creates a program that includes a new file DIFFSIZES.inc, containing information about array sizes. Precisely, the include file must declare the integer constant nbdirsmax which is the maximum number of differentiation directions that you plan to compute in a single run. nbdirsmax is used in the declarations of the size of the differentiated arrays. You must create this file DIFFSIZES.inc before starting the second differentiation step. For instance, this file may contain
```
       integer nbdirsmax
       parameter (nbdirsmax = 50)
```
if 50 is the max number of differentiation directions. If what you want is the Hessian, this max number of differentiation directions is the cumulated sizes of all the inputs x.
The second multi-directional differentiation requires a new maximum size value nbdirsmax0, which is a priori different from nbdirsmax. For the Hessian case, it is probably equal to nbdirsmax. What's more, Tapenade has inlined the 1st level include file, so what you get is a strange looking piece of declarations:
```
      ...
      INCLUDE 'DIFFSIZES.inc'
C  Hint: nbdirsmax should be the maximum ...
      INTEGER nbdirsmax
      PARAMETER (nbdirsmax=50)
      ...
```
We suggest you just remove the INCLUDE 'DIFFSIZES.inc' line, and hand-replace each occurrence of nbdirsmax0 by either nbdirsmax or even 50!
A complete Hessian is in general symmetric. Tapenade was not able to take advantage of this. You may do so by replacing every successive lines of the form
```
      ...
      DO nd=1,nbdirs
        DO nd0=1,nbdirs0
      ...
```
by
```
      ...
      DO nd=1,nbdirs
        DO nd0=nd,nbdirs0
      ...
```

TANGENT-ON-REVERSE APPROACH:

Suppose the output y is scalar. Then you know that the reverse mode of AD can return you with the Jacobian, which is a single-row matrix, i.e. a gradient, at a very low cost. The natural extension of this is to differentiate the reverse-differentiated program, this time in multi-directional tangent mode. Hence the name "Tangent-on-Reverse". In theory, the cost of computing the gradient is a fixed small multiple (say 7*) of the cost of the original program P. Similarly, the cost of computing the tangent derivative is also a small multiple (say 4*) of the cost of P. If one uses the multi-directional tangent mode, for n simultaneous directions, the cost of the multi-directional tangent derivative is proportional to n (say 4*n). To summarize, the cost of computing the complete Hessian through the Tangent-on-Reverse approach should be roughly


              4*n*7*P

whereas the cost of computing the complete Hessian through the Tangent-on-Tangent approach should be roughly


              4*n*4*n*P

Therefore Tangent-on-Reverse is appealing, although in reality things are not so clear-cut.

Tangent-on-Reverse raises a number of new problems, because of the PUSH and POP that are inserted by reverse differentiation. To obtain an correct tangent differentiation, one must tell the second-step Tapenade about the behavior of these PUSH and POP added by the first-step Tapenade. This could be improved if Tapenade made the two steps jointly, but this is still not the case...
First thing is to declare the inputs and outputs of PUSH and POP. In addition to their argument, they have another hidden parameter, which is the stack. You must declare this in a special file, using the syntax for black-box routines described here. We provide such a file, named PUSHPOPGeneralLib, in the ADFirstAidKit. You may need to extend it if it doesn't cover a PUSH or POP function that your code uses.
You will tell Tapenade to use this file PUSHPOPGeneralLib in the command line, using the command-line option


  ... -ext PUSHPOPGeneralLib ...

The second thing is to link the final Tangent-on-Reverse differentiated code with PUSHPOPDiff.o obtained by compiling PUSHPOPDiff.f.

PUSHPOPGeneralLib declares the inputs and outputs of the PUSH and POP procedures. For example the lines
```
subroutine popreal8:
  external:
  shape:(param 1,
         common /adstack/[0,*[)
  type:(modifiedTypeName(modifiers(intCst 8), float()),
        arrayType(modifiedTypeName(modifiers(intCst 8), float()),
                  dimColons(dimColon(none(),none()))))
  ReadNotWritten: (0, 0)
  NotReadThenWritten: (1, 0)
  ReadThenWritten: (0, 1)
  deps: (0, 1,
         0, 1)
```
mean that POPREAL8 has indeed two arguments. One is the formal parameter, which is a REAL*8, and the other is the stack, whose type is an array of REAL*8 values. The formal parameter is not read but overwritten, the stack is read and overwritten i.e. modified. PUSHPOPGeneralLib also declares the dependencies through the PUSH and POP procedures. For example the lines concerning POPREAL8
```
  deps: (0, 1,
         0, 1)
```
mean that POPREAL8 outputs a value in its first argument that only depends on the given value of the stack, and also sets a new value for the stack that only depends on the given value of the stack.
You may need to add new such declarations if your code uses other PUSH and POP's, such as PUSHREAL4.
PUSHPOPDiff.f defines the differentiated procedures for the PUSH and POP procedures, in plain tangent mode as well as in multi-directional tangent mode. These differentiated routines exist only for the PUSH and POP of active variables. In particular there are no such differentiated routines for PUSHINTEGER nor POPINTEGER. The trick is to push and pop the original variable and the differentiated variable, and since we use a stack, the order of the PUSH'es and POP's is reversed. You may need to add new such definitions if your code uses other PUSH and POP's, such as PUSHREAL4.

This complete process is still very much experimental, so be aware that errors might occur. Don't hesitate to contact us through the Tapenade mailing list in case of trouble (subscribe

to the "tapenade-users" mailing list).

Differentiating MPI:

Can Tapenade handle MPI parallel code?
What is the AMPI library?

Tapenade can handle a useful subset of the MPI primitives, using a special library called AMPI. AMPI is a wrapper around MPI, that in addition provides mechanisms for differentiation of a ``large enough'' subset of MPI. AMPI stands for Adjoinable MPI.

Using AMPI is a three steps process. The end-user must first transform their source so that it uses AMPI instead of MPI. This transformation is lightweight, basically changing MPI calls by adding a A in front, and a few other modifications. Most importantly, AMPI point-to-point communication calls require extra arguments, needed by AD, to provide information about the other end of the communication. The resulting, hand-transformed, AMPI source code must compile and run exactly like the original MPI source. It is important to check this identity before trying any differentiation.

In the second step, the end-user can differentiate the AMPI source code with Tapenade. (Note that turning your MPI source into AMPI enables you to differentiate it also with OpenAD, AdolC, or dco). With Tapenade, you can apply tangent or adjoint AD. As usual but even more in the case of MPI, we strongly recommend that you first test AD in tangent mode before switching to adjoint AD.

In the third step, the AMPI differentiated source can be compiled and run. This requires to link with the compiled AMPI library, and also with Tapenade-specific AMPI support files named ampiSupport.c and (in the FORTRAN case) fortranSupport.F. Both are provided in the ADFirstAidKit directory of your local installed Tapenade files.

AMPI does not cover the full latest MPI: it covers most of point-to-point communications and collective communications. AMPI covers user-defined communicators and MPI types, at least as far as we tested. On the other hand, AMPI does not cover one-sided communications.

AMPI was developed in collaboration with Argonne National Lab (Argonne, IL, USA) and is available from their repository at:
https://www.mcs.anl.gov/~utke/AdjoinableMPI/AdjoinableMPIDox/UserGuide.html
The main developer of AMPI is Jean Utke, with contributions from Michel Schanen, Sri Hari Krishna Narayanan, Anton Bovin, and Laurent Hascoet. In many respects, AMPI should still be considered experimental. The same holds for Tapenade AD on AMPI source. Reports are welcome.

FIRST STEP: INSTALL AND SWITCH TO AMPI

Download AMPI from their repository and install it on your computer. Follow the installation steps indicated in the AMPI documentation. The installation steps depend on the actual MPI that you use (we usually test with mpich and with openMPI). To illustrate, here is a sequence of commands for installation with mpich, for intended differentiation on FORTRAN or C source. If you work exclusively with C, you may omit the configure/make steps about F77. If you work exclusively with FORTRAN, you may omit the configure/make steps about C:


$> PATH=$PATH:your_MPI_installation_directory/bin
$> LD_LIBRARY_PATH=your_MPI_installation_directory/lib:$LD_LIBRARY_PATH
$> export MPIRUN="mpirun -host localhost"
$> export AMPIINST=your_AMPI_installation_directory
$>
$> cd your_AMPI_source_directory/AdjoinableMPI
$> ./autogen.sh
$> ./configure  --prefix=$AMPIINST/AMPI4C
$> make all install
$> ./configure  --prefix=$AMPIINST/AMPI4F77 --enable-fortranCompatible
$> make all install

About switching to AMPI:

Include AMPI instead of MPI, i.e. in FORTRAN replace any use mpi or include 'mpif.h' with include 'ampi/ampif.h', while in C replace #include <mpi.h> with #include "ampi/ampi.h"
Turn types MPI_Request into AMPI_Request
Prepend a ``A'' in front AND append a ``_NT'' at the end of all MPI_Init, MPI_Finalize, MPI_Type_contiguous, MPI_Type_create_struct, MPI_Type_create_resized, MPI_Type_commit, MPI_Type_free, MPI_Op_create, MPI_Op_free, MPI_Comm_split, MPI_Comm_create, MPI_Comm_dup, MPI_Comm_free
Prepend a ``A'' in front of all MPI_Comm_rank, MPI_Comm_size, MPI_Get_processor_name, MPI_Pack_size , of all point-to-point (MPI_Send, MPI_Isend, MPI_Rsend, MPI_Bsend, MPI_Recv, MPI_Irecv, MPI_Wait, MPI_Waitall...), and of all collectives (MPI_Barrier, MPI_Bcast, MPI_Reduce, MPI_Allreduce, MPI_Gather, MPI_Allgather, MPI_Scatter, MPI_Gatherv, MPI_Allgatherv, MPI_Scatterv...)
Add the extra argument (before the communicator argument) to all send and recv that indicates the kind of the other end of communication.
For any send, the extra argument may be AMPI_TO_RECV, AMPI_TO_IRECV_WAIT, AMPI_TO_IRECV_WAITALL.
For any recv, the extra argument may be AMPI_FROM_SEND, AMPI_FROM_ISEND_WAIT, AMPI_FROM_ISEND_WAITALL, AMPI_FROM_BSEND, AMPI_FROM_RSEND.

After switching to AMPI, don't forget to check that the transformed source (e.g. programAMPI.c or programAMPI.f) compiles and behaves the same as the non-transformed source. If the source is in C, commands may look like:


$> export AMPIROOT=$AMPIINST/AMPI4C
$> mpicc -I$AMPIROOT/include -o exeAMPI programAMPI.c -L$AMPIROOT/lib -lampiPlainC -lm 
$> LD_LIBRARY_PATH=$AMPIROOT/lib/:$LD_LIBRARY_PATH ; mpirun -host localhost -np 4 exeAMPI

If the source is in FORTRAN, commands may look like:


$> export AMPIROOT=$AMPIINST/AMPI4F77
$> mpif77 -I$AMPIROOT/include -c fortranSupport.F -o fortranSupport.o 
$> mpif77 -I$AMPIROOT/include programAMPI.f fortranSupport.o -o exeAMPI -L$AMPIROOT/lib -lampiPlainC -lm 
$> LD_LIBRARY_PATH=$AMPIROOT/lib/:$LD_LIBRARY_PATH ; mpirun -host localhost -np 4 exeAMPI

SECOND STEP: DIFFERENTIATE

We recommend you try tangent mode first, and we recommend you use the -context option to ease validation and debug (caution, long lines wrapped...):


$>  tapenade programAMPI.c -I your_MPI_include_directory -I $AMPIROOT/include -d \
         -context -fixinterface -o programAMPI any_other_option_you_may_need

When you are satisfied with the tangent, you may go for the adjoint (caution, long lines wrapped...):


$>  tapenade programAMPI.c -I your_MPI_include_directory -I $AMPIROOT/include -b \
         -context -fixinterface -o programAMPI any_other_option_you_may_need

Notice the include paths to tell Tapenade where are the MPI and AMPI include files. If in FORTRAN, just replace programAMPI.c with programAMPI.f.

If you provide a code complete with its main procedure, the -context option will give you a complete differentiated code with its main procedure, that you can compile and run.

WARNING:

In adjoint mode, there is (at least) one big feature missing: at every ``turn'' point, i.e. when the forward sweep ends and the backward sweep starts, for every variable V that was sent or received by a non-blocking AMPI_Isend or AMPI_Irecv, and this communication is active (i.e. Tapenade has set a reverse communication of the derivative Vb), then a special procedure must be called at the turn point:


ADTOOL_AMPI_Turn(V, Vb)

Automatic insertion of those by Tapenade is not implemented yet. Sorry.

THIRD STEP: COMPILE AND RUN

We assume you have provided Tapenade with a source complete with its main procedure, and you have used the -context option. Therefore programAMPI_d.c (or _b, or .f) is complete with its main procedure.

See the "validation" FAQ entry for details about the -context option and the resulting validation process of the differentiated code, using the DBAD_PHASE shell variable. Because this is MPI, the file that defines this validation mechanism triggered by -context had to be adapted: you must link with adContextMPI.c instead of adContext.c. This file is in the ADFirstAidKit as well.

Remember that fortranSupport.F, ampiSupport.c, adContextMPI.c, adStack.c are all found in the ADFirstAidKit.

If the source is in C, commands to run (and validate) the tangent may look like (caution, long lines wrapped...):


$> export AMPIROOT=$AMPIINST/AMPI4C
$> mpicc -I$AMPIROOT/include -c ampiSupport.c -o ampiSupport.o
$> mpicc -IADFirstAidKit -I$AMPIROOT/include programAMPI_d.c \
         ampiSupport.o adStack.c adContextMPI.c -L$(AMPIROOT)/lib \
         -lampiCommon -lampiBookkeeping -lampiPlainC -lm -o tgtAMPI
$> export DBAD_PHASE=1
$> LD_LIBRARY_PATH=$AMPIROOT/lib/:$LD_LIBRARY_PATH ; mpirun -host localhost -np 4 tgtAMPI
$> export DBAD_PHASE=2
$> LD_LIBRARY_PATH=$AMPIROOT/lib/:$LD_LIBRARY_PATH ; mpirun -host localhost -np 4 tgtAMPI

and then, if all goes well, for the adjoint (caution, long lines wrapped...):


$> mpicc -IADFirstAidKit -I$AMPIROOT/include programAMPI_b.c \
         ampiSupport.o adStack.c adContextMPI.c -L$AMPIROOT/lib \
         -lampiCommon -lampiBookkeeping -lampiPlainC -lm -o adjAMPI 
$> LD_LIBRARY_PATH=$AMPIROOT/lib/:$LD_LIBRARY_PATH ; mpirun -host localhost -np 4 adjAMPI

If the source is in FORTRAN, commands to run (and validate) the tangent may look like (caution, long lines wrapped...):


$> export AMPIROOT=$AMPIINST/AMPI4F77
$> mpif77 -I$AMPIROOT/include -c fortranSupport.F -o fortranSupport.o 
$> mpicc -I$AMPIROOT/include -c ampiSupport.c -o ampiSupport.o
$> mpif77 -IADFirstAidKit -I$AMPIROOT/include programAMPI_d.f \
         ampiSupport.o fortranSupport.o adStack.c adContextMPI.c -L$AMPIROOT/lib \
         -lampiCommon -lampiBookkeeping -lampiPlainC -lm -o tgtAMPI 
$> export DBAD_PHASE=1
$> LD_LIBRARY_PATH=$AMPIROOT/lib/:$LD_LIBRARY_PATH ; mpirun -host localhost -np 4 tgtAMPI 
$> export DBAD_PHASE=2
$> LD_LIBRARY_PATH=$AMPIROOT/lib/:$LD_LIBRARY_PATH ; mpirun -host localhost -np 4 tgtAMPI

and then, if all goes well, for the adjoint (caution, long lines wrapped...):


$> mpif77 -IADFirstAidKit -I$AMPIROOT/include programAMPI_b.f \
         ampiSupport.o fortranSupport.o adStack.c adContextMPI.c -L$AMPIROOT/lib \
         -lampiCommon -lampiBookkeeping -lampiPlainC -lm -o adjAMPI 
$> LD_LIBRARY_PATH=$AMPIROOT/lib/:$LD_LIBRARY_PATH ; mpirun -host localhost -np 4 adjAMPI

Declarations improperly differentiated:

The array dimensions are lost in the differentiated declaration.

Common containing arrays:
If an array has its bounds declared in the common statement, the differentiated declarations may lost these bounds. If it is the case, you should declare these bounds in the type declaration statement instead of the common statement.

The pointer, target, and allocatable statements:


allocatable :: a(:,:)
pointer :: son
target :: a, y(10)

As described In "Fortran 95/2003 explained", "We believe that it is much clearer to specify these attributes on the type declaration statements, and therefore do not use these forms."
In particular, if these statements use implicit typing, some declarations may be differentiated improperly.
Until we fix these bugs, you should completly declare the arrays or allocatable arrays in the typing declaration.

Errors on complicated statements:

I got the message (TC43) Could not find type of ..., please check

For differentiation purposes, Tapenade sometimes needs to split a long and complex expression with subroutine calls, introducing a a number of new intermediate variables. Usually this works fine, but in some situations, Tapenade cannot guess the type and size of the new intermediate variable. If Tapenade fails to find the correct type REAL of the temporary variable, puts INTEGER instead, this looses activity. We put the warning message (TC43) to signal the problem. The workaround is to do the splitting beforehand, on the source program, and to declare the intermediate variables with the correct type.

Copied procedures in the differentiated code :

Tapenade generates a large body of what looks like superfluous code that simply duplicates the code going in to Tapenade.

There are nearly-copies of the original procedures in the differentiated code. They appear in general with a new name obtained by appending "_C". This happens in FORTRAN90 when a non-differentiated subroutine USE's a differentiated MODULE.
Suppose the original code is:


MODULE M
  ...
END MODULE M

SUBROUTINE S
USE M
...
END SUBROUTINE S

This code is differentiated as:


MODULE M_DIFF
  ...
END MODULE M_DIFF

SUBROUTINE S_B
USE M_DIFF
...
END SUBROUTINE S_B

SUBROUTINE S_NODIFF
USE M_DIFF
...
END SUBROUTINE S_NODIFF

Subroutine "S_NODIFF" is a copy of subroutine "S": it is not differentiated, but it USE's the differentiated module "M_DIFF" instead of the original module "M". So this does not create a clash for users who use the original code together with the differentiated code: we generate a different procedure for "S".
So we chose to make a difference between

"S", the original "S" that works with the original "M", and
"S_NODIFF", the copy of "S" for the reverse mode, which works with the same module "M_DIFF" as the differentiated "S_B".

This causes code almost-duplication but fewer compilation conflicts.
Another naming convention was used before 2017: to retrieve this convention, add command-line options:
-tgtmodulename "_d" -adjmodulename "_b" -copyname "_c"

Principal command-line arguments :

What are the main command-line arguments that I can use?
What can I specify about differentiation heads?

Typing


  tapenade -help

gives you a list of command-line arguments. Here are the most important:

-head description lets you specify with great detail the differentiation heads, i.e. the subroutines that define the functions that you want to differentiate, along with the independent and dependent variables with respect to which you want to differentiate. The simplest use case is -head foo, that declares procedure foo as one head, and differentiates all of its outputs with respect to all of its inputs. The description can describe more sophisticated goals, see this section for details.
-d triggers the tangent mode of AD, also known as directional or direct mode.
-b triggers the adjoint mode of AD, also known as reverse mode.
-vector modifies the selected mode (tangent or adjoint) to make it multi-directional, i.e. run in several (adjoint) directions at a time. See details here.
-p only analyzes the code. Does not differentiate it. Produces a copy of the code. This copy contains additional comments that show the result of pointer destination analysis.
-o filename tells Tapenade to place all output code into a single file named after filename. For instance, if this is a Fortran file, and adjoint differentiation has beed requested, the output file will be named filename_b.f.
-O dir tells Tapenade to place all output files into directory dir.
-tgtvarname pattern, -tgtfuncname pattern, -adjvarname pattern, -adjfuncname pattern let you modify the default naming of tangent and adjoint variables and procedures.
For instance -tgtvarname %diff will systematically name the tangent derivative of a variable named myvar as myvardiff. Similarly, -adjfuncname adj_%_g will systematically name the adjoint derivative of a procedure named foo as adj_foo_g.
-inputlanguage lang, -outputlanguage lang let you specify the language of the input files, and the desired language of the differentiated files. lang may be one of fortran, fortran90, fortran95, or C. Using this option may help Tapenade make some system-related decisions, call the right parser, or disambiguate other dubious cases. However these options must be used sparingly:
- The input language is in general deduced from the file names, so there's no point in specifying it explicitly.
- The output language should most often be the same as the input's. Using a different output language might be fun or interesting, but seldom produces correct code
See details here.
-ext filename loads filename as a description of some intrinsics that are used by the given code, but not currently described in the "standard" Tapenade libraries. See details here
-nolib deactivates loading of the standard libraries that tell Tapenade about the intrinsics of the input language. See details here
-isize, -rsize, -drsize, -psize let you specify the actual size on the target system for integers, reals (i.e. floats), double precision reals (i.e. double floats), and pointers respectively. This is important for computing offsets in COMMON blocks, and to determine sizes for the PUSH and POP operations used in adjoint mode. For instance -r8 says that the size for reals is 8 bytes (and therefore 16 for double precision reals). See details here

The command-line arguments to the tapenade command consist of one or many file names and of zero or many of the above options, all of these coming in any order. If an option is not recognized, it is treated as a filename, which may result in a "file not found" exception.

Building the context for calling the differentiated code :

I have differentiated my root procedure. How should I organize the program that calls it?
I'm lost with these all these FOO and FOO_D and FOO_CD procedures and modules. How can I include them into my big application?
My differentiated program does a segmentation fault because some differentiated globals are not allocated!

The following is yet subject to discussions and modifications, which means it may change sorry ! Tapenade differentiates the call tree that is under the root procedure that you have specified. The result is a set of differentiated modules and/or differentiated standalone procedures, that do not execute alone but must be used/called from a certain context. It is up to you to write this calling context, and Tapenade can help you only to a certain point. The following discussion focuses on the tangent mode. Be aware that things can be slightly harder in the adjoint mode.

You may use as a basis a calling context designed for the original, non-differentiated root procedure. Notice that even if you provided Tapenade with the complete calling context code as well, it will differentiate only the call graph below the root procedure. The calling context will not be modified nor adapted to the differentiated root. So even if there is a calling context available for the root, you will have to modify it by hand so that it can call the differentiated root.

There are many possibile cases, so we'd rather use an example. We'll try to extract general rules later. Here's a small example source program. The differentiation root procedure is ROOT. The first column contains the code that is not in the call graph below ROOT.


PROGRAM MAIN
  USE MMA
  USE MMB
  REAL, DIMENSION(:), ALLOCATABLE :: x
  INTEGER :: i
  REAL :: cva(2)
  COMMON /cc1/ cva
  EXTERNAL GETFLAG
  CALL GETFLAG(flag)
  ALLOCATE(x(30))
  CALL INITA()
  DO i=1,20
    aa(i) = 100.0/i
    x(i) = 3.3*i
  END DO
  cva(1) = 1.8
  cva(2) = 8.1
  CALL ROOT(x)
  PRINT*, 'zz=', zz
  DEALLOCATE(aa)
  DEALLOCATE(x)
END PROGRAM MAIN


MODULE MMA
  REAL, DIMENSION(20), ALLOCATABLE :: aa

CONTAINS
  SUBROUTINE INITA()
    ALLOCATE(aa)
  END SUBROUTINE INITA
END MODULE MMA

MODULE MMB
  INTEGER :: flag
  REAL :: zz
END MODULE MMB

SUBROUTINE ROOT(x)
  USE MMA
  USE MMB
  REAL, DIMENSION(*) :: x
  REAL :: v
  REAL :: cv1, cv2
  COMMON /cc1/ cv1, cv2
  zz = cv1*cv2
  v = SUM(aa)
  IF (flag .GT. 2) zz = zz*v
  zz = zz + SUM(x)
END SUBROUTINE ROOT

We will differentiate in tangent mode, with head ROOT. We will not specify the name of the output file, so that every module or isolated procedure of the differentiated code will be put into a separate file. The differentiated call graph is returned in files root_d.f90, mma_d.f90, and mmb_d.f90.

root_d.f90 defines procedure ROOT_D mma_d.f90, mmb_d.f90 define modules MMA_D, MMB_D


!  Diff. of root in tangent mode:
!   variations of useful results: zz
!   with respect to varying inputs:
!    *aa cv1 cv2 x
!   RW status of diff variables:
!    zz:out *aa:in cv1:in cv2:in x:in
SUBROUTINE ROOT_D(x, xd)
  USE MMB_D
  USE MMA_D
  IMPLICIT NONE
  REAL, DIMENSION(*) :: x
  REAL, DIMENSION(*) :: xd
  REAL :: v
  REAL :: vd
  REAL :: cv1, cv2
  REAL :: cv1d, cv2d
  COMMON /cc1/ cv1, cv2
  INTRINSIC SUM
  COMMON /cc1_d/ cv1d, cv2d
  zzd = cv1d*cv2 + cv1*cv2d
  zz = cv1*cv2
  vd = SUM(aad)
  v = SUM(aa)
  IF (flag .GT. 2) THEN
    zzd = zzd*v + zz*vd
    zz = zz*v
  END IF
  zzd = zzd + SUM(xd)
  zz = zz + SUM(x)
END SUBROUTINE ROOT_D


MODULE MMA_D
  IMPLICIT NONE
  REAL, DIMENSION(:), ALLOCATABLE :: aa
  REAL, DIMENSION(:), ALLOCATABLE :: aad

CONTAINS
  SUBROUTINE INITA()
    IMPLICIT NONE
    ALLOCATE(aad(20))
    ALLOCATE(aa(20))
  END SUBROUTINE INITA
END MODULE MMA_D

MODULE MMB_D
  IMPLICIT NONE
  INTEGER :: flag
  REAL :: zz
  REAL :: zzd
END MODULE MMB_D

The calling context of the original ROOT is not sufficient to call ROOT_D and must be adapted. Here this context consists of program MAIN, but there can be more modules and procedures in it. The new program MAIN_CD produced by Tapenade in file main_cd.f90 is a possible starting point, but it must be modified by hand. Or you can write it from scratch. For instance:


PROGRAM MAIN_CD
  USE MMB_D
  USE MMA_D
  REAL, DIMENSION(:), ALLOCATABLE :: x
  REAL, DIMENSION(:), ALLOCATABLE :: xd
  INTEGER :: i
  REAL :: cvad(2)
  COMMON /cc1_d/ cvad
  REAL :: cva(2)
  COMMON /cc1/ cva
  EXTERNAL GETFLAG
  CALL GETFLAG(flag)
  ALLOCATE(xd(30))
  ALLOCATE(x(30))
  CALL INITA()
  initialize aad,xd,cvad,zzd
  DO i=1,20
    aa(i) = 100.0/i
    x(i) = 3.3*i
  END DO
  cva(1) = 1.8
  cva(2) = 8.1
  CALL ROOT_D(x, xd)
  PRINT*, 'zz=', zz, 'and zzd=', zzd
  DEALLOCATE(aad)
  DEALLOCATE(aa)
  DEALLOCATE(xd)
  DEALLOCATE(x)
END PROGRAM MAIN_CD

Places of interest are in blue. Some comments:

the context must call the differentiated root, hence the call to ROOT_D.
the context must provide ROOT_D with all the derivatives of its arguments, whether formal parameters or globals. Hence xd, but also aad, /cc1_d/, zzd.
These new xd, aad, /cc1_d/, zzd must be declared, allocated if their original variable is, and initialized with the derivatives you want.
After return from ROOT_D, the derivatives in these variables can be used, and the variables must be deallocated if their original variable is.
One must make sure that these variables are effectively the same in the context and in ROOT_D, which means that when they are globals from modules, the same modules must be used on both sides. Hence the USE MMA_D and USE MMB_D. This also ensures that the "good" INITA() is called.
All these operations need not be done only in MAIN_CD. If MAIN_CD calls utility procedures, you may choose to modify these procedures instead. Make sure to keep all these modified procedures separated from their original definition, and link with the original code only when it was not modified. This also applies to MAIN_CD itself.
To make sure you don't mix the original context procedures and the new context procedures adapted to ROOT_D, why not give them the same procedure name? This way, the compiler should complain if you mix them. Here MAIN_CD could just remain MAIN. The same could be said for module names MMA_D and MMB_D but that's another story as currently Tapenade systematically appends a _D to them.

Tapenade and Windows :

What should I do to use Tapenade on Windows?

Before installing Tapenade, you must check that an up-to-date Java Runtime Environment is installed. If there is none, you can download and install the latest Java Runtime Environment (Java SE 8 or JDK8) from the java.sun.com site. Tapenade will not run with an older Java Runtime Environment.

Then

If not already done, read our download page.
As instructed in the Windows section of the README.html, download the tapenade zip archive (tapenadeN.m.zip, where N.m is the current version number) into your chosen installation directory install_dir
Go to your chosen installation directory install_dir, and extract TAPENADE from the zip file.
Save a copy of the install_dir\tapenadeN.m\bin\tapenade.bat file and modify install_dir\tapenadeN.m\bin\tapenade.bat according to your installation parameters:
replace TAPENADE_HOME=.. by TAPENADE_HOME=install_dir\tapenadeN.m
replace JAVA_HOME="C:\Progra~1\Java\jdkXXXX" by your current java directory
replace BROWSER="C:\Program Files\Internet Explorer\iexplore.exe" by your current browser.

Even if you don't have cygwin installed, take a look also at the section on cygwin-related problems.

Tapenade, Windows and Cygwin problems :

Under Windows, Tapenade cannot parse my fortran file.
I tested by hand my fortranParser.exe on a Fortran file and I got no output at all.
or when parsing a Fortran file with Tapenade, I get these error messages :


You have multiple copies of cygwin1.dll on your system.
Search for cygwin1.dll using ...
and delete all but the most recent version. The most recent version *should*
reside in x:\cygwin\bin, where 'x' is the drive on which you have
installed the cygwin distribution.
System: Parsing error

The Fortran parser of Tapenade fortranParser.exe, called separately on a correct Fortran file, should return a sequence of (mostly) numbers.
If it returns nothing or an error message like the one above, it may be because of the cygwin1.dll that it uses.
The Tapenade distribution provides a cygwin1.dll, in the folder tapenade/bin/windows.

If your system has a more recent cygwin1.dll already installed, just remove the one provided by Tapenade, which is too old.
Conversely, if there is no cygwin1.dll found using the system path, you should put one back, e.g. into the cygwin bin folder.

Tapenade with C programs on Windows and Mac OS X, Syntax Errors:

Lexical and syntax errors, java errors

Before parsing a C program, Tapenade calls cpp to preprocess the C program. On a unix machine, cpp is found in the standard PATH. You can specify the cpp command using the option -cpp "/.../.../cpp_command". On a windows machine, if you have cygwin, you should find the correct path.
Tapenade fails when using the preprocessor of the new release of Mac OS X 10.9 Mavericks and Xcode 5. In this case, please preprocess your files before sending them to Tapenade and call tapenade -cpp "nocpp" program.c to avoid the automatic call to "cpp".

Validation of the differentiated programs (MANUAL METHOD)

This section describes our suggested manual method for validation. Our hope is that you don't need to go through it, but rather use this automated validation method provided since the end of 2017. Come back here only if the automated validation is not enough for your needs.

This is a difficult issue. Differentiated programs are very long and complex and you may find it hard to check them by hand, even if we try to keep them readable. Here is a proposed method to validate/debug the code produced by Tapenade. It uses Tapenade options that are available only in the command-line version (local installation). It also uses two files that are in the ADFirstAidKit directory of your local installed Tapenade files. If you don't have a locally installed Tapenade, please follow these steps. Also, to ease our validation mechanism, we strongly advise you to follow a few preparation steps, before you even start to differentiate anything. Validation is by no means easy. Although we try to automate the process, it still requires good knowledge of the principles of AD, especially for the adjoint mode. The sad thing with Tapenade's validation mechanism is that you may run into bugs of Tapenade itself (otherwise you wouldn't be reading this section anyway!) but you may also run into bugs of the validation mechanism itself.

In the following, words between double quotes and drawn in this color (such as "SHAPE") are indeed templates, that must be instantiated by actual strings depending on the context. Square brackets represent additional arguments, and the star represents repetition.
In the example pieces of programs, actual pieces of code are written in this sort of dark red, short strings in double quotes are "patterns" as above, and

      "entiere lines between double quotes and drawn in the pattern color"

describe a piece of code that you must write at that place.

The choice of Independent and Dependent parameters may interfere with the validation process. This is explained at the end of this section, but we'd rather warn you right now. Make sure you read this part if validation fails close to the entry-into or exit-from your code. We assume the root of the differentiated code is a procedure P(X,Y), where X is the input and Y the output. Therefore Tapenade produces an AD tangent which is a procedure P_D(X,Xd,Y,Yd), and an AD adjoint which is a procedure P_B(X,Xb,Y,Yb). Generalization to many inputs or outputs or to a function is straightforward.

CHECK THE SIZES OF PRIMITIVE TYPES:

If the program crashes, there is a small chance that this comes from the sizes of basic types on your system. To test these sizes, go into the ADFirstAidKit directory, then:

1) adapt the compilation commands $(FC) and $(CC) in the Makefile
2) make testMemSize
3) execute testMemSize
4) look at the sizes printed.

CHECK THE TANGENT DERIVATIVES WITH RESPECT TO DIVIDED DIFFERENCES:

Mathematical principle: Comparison with divided differences is the standard way to test the tangent derivatives. It amounts to running your original subroutine P twice, once with a perturbed input X+*Xd, once with X, and then computing: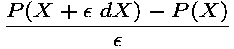

You should get nearly the same result as the Yd returned by tangent differentiated subroutine P_D(X,Xd,Y,Yd) With a "good" epsilon, differences should be only on a few last decimals. There is a lot to say on the choice of a good epsilon. It depends on the algorithm, the data ... and maybe also the phase of the moon. Also, it is certainly more accurate to compute the centered divided differences, but we generally don't need this degree of accuracy for our validation.

Testing principle: We will run simultaneously two instances of the differentiated code, augmented with special debugging calls at selected locations.

The first instance, called "codeDD1", runs P_D on input X+epsilon*Xd, for some small epsilon. Since it runs P_D, "codeDD1" also computes derivatives, but we will not use them.
The second instance, called "codeDD2", runs P_D on input X.

At selected run-time locations in the code, for any selected variable of interest v at this location, codeDD1 sends out the value of v to codeDD2.
On its side, at the corresponding run-time location in the code, for the same variable of interest v at this location, codeDD2 receives the value sent by codeDD1 into a temporary variable veps and uses it to compute vd_approx = (veps - v)/epsilon Since codeDD2 actually runs P_D, it also has available in variable vd the current value of the tangent derivative of v at this location.
Therefore codeDD2 just needs to test for approximate equality between vd_approx and vd, and send a message if the test fails.

Testing process: To run the test, start from the prepared code according to the recommended code preparation. Suppose the "central" part looks like:


          ... whatever code is before ... 
C Beginning of the procedure to differentiate
       CALL MYFUNC(x1, x2,..., y1, y2,...)
C End of the procedure to differentiate
          ... whatever code comes after ...

Define two copies of your complete code, that will differ only in this "central" part.

The first copy, that we will call "codeDD1", compiles into an executable that we will call "exeDD1". In "codeDD1", instead of calling MYFUNC, you must call its tangent differentiated version MYFUNC_D, and you must place a few debugging primitives before and after, as follows:


          ... whatever code is before ... 

          Now initialize the input differentiated variables, to 
          define the chosen differentiation direction, e.g.:
       x1d = 1.5d0
       x2d = (/-1.d0,2.3d0,-0.5d0,.../)
          ...
          Now prepare for the test:
       CALL DEBUG_TGT_INIT1(1.d-8, 1.d-5, .1d0)
       CALL DEBUG_TGT_INITREAL8(x1, x1d)
       CALL DEBUG_TGT_INITREAL8ARRAY(x2, x2d, ns)
          ...
       CALL DEBUG_TGT_CALL('MYFUNC', .true., .false.)
C Beginning of differentiated part
       CALL MYFUNC_D(x1, x1d, x2, x2d, ..., y1, y1d, y2, y2d, ...)
C End of differentiated part
          Now terminate the test:
       CALL DEBUG_TGT_EXIT()
       CALL DEBUG_TGT_CONCLUDEREAL8('y1', y1, y1d)
       CALL DEBUG_TGT_CONCLUDEREAL8ARRAY('y2', y2, y2d, 20)
          ...

          ... whatever code comes after ...

The second copy, that we will call "codeDD2", compiles into an executable that we will call "exeDD2". You must make it identical to "codeDD1" except that you will call DEBUG_TGT_INIT2 instead of DEBUG_TGT_INIT1

A few remarks and explanations:

Each copy "codeDD1" and "codeDD2" will be executed independently. Each must use or read from the same data files as the original code, and should behave exactly the same until reaching the central part. You don't need to duplicate every source file to define these copies "codeDD1" and "codeDD2". You probably need only to duplicate the file that contains the "central" part. The rest should be taken care of by the compilation and link commands.
The code for MYFUNC_D must be built by Tapenade by tangent differentiation of the source code, with the only additional command-line option -debugTGT. The same differentiated code is used by "exeDD1" and "exeDD2".
Each executable "exeDD1" and "exeDD2" must be linked with the debugging library provided in the "First-Aid Kit". This library consists of file debugAD.f and its include file debugAD.inc
The calls to DEBUG_TGT_INIT1 or to DEBUG_TGT_INIT2 must have the same arguments. The first is the "epsilon" used for divided differences. The second is called "almost-zero" (see below). The third is the "threshold" (see below) error percentage above which a message is printed.
In the prepared code above, notice that there is a statement that initializes each input differentiated variable. You are free to choose the values, therefore choosing the direction of your tangent. Naturally, you must provide the same values for "codeDD1" and "codeDD2". Naturally, arrays require several values.
A few lines later, before calling MYFUNC_D, you must insert one initialization call for each input differentiated variable. For arrays, initialization procedure DEBUG_TGT_INITREAL8ARRAY takes an extra argument, which is the size of the array. For single precision REAL's, replace REAL8 by REAL4.
The same remarks apply to the DEBUG_TGT_CONCLUDE... debug termination calls.
Don't forget to declare all used differentiated variables, in the declaration part of your codes "codeDD1" and "codeDD2".
The new differentiation invocation (Tapenade called with the additional command-line option -debugTGT) may cause additional messages printed, that ask e.g. for the size of array dimensions. These messages must be taken care of, in the way explained in this FAQ: see the section about the particular message.

When "exeDD1" and "exeDD2" are ready, run the divided differences test by just typing the command line:


   $> exeDD1 | exeDD2

using a UNIX pipe "|" (or equivalent). What happens behind the scene is: exeDD1 runs on the input "plus epsilon times direction". At selected moments ("points" in execution), it calls procedures such as DEBUG_TGT_REAL8, which send the value of selected variables into std-out, therefore into the pipe.
In parallel, exeDD2 runs on the input "without epsilon". At the same selected points, it also calls procedures such as DEBUG_TGT_REAL8, which has now a different behavior: it reads the value of the same selected variables from std-in, therefore from the pipe. Using its own value of the same variable, it computes de derivative approximation by divided differences (the "DD derivative") and compares it with the analytical derivative. If the DD derivative is almost zero (i.e. absolute value below the given "almost-zero"), the comparison is not done because Tapenade code sometimes doesn't reinitialize zero derivatives (to save time). Otherwise, if the percentage of difference is more that the "threshold", a message is printed on the screen.

Interpreting the test result: What you obtain on the screen looks like what follows. In this example, we introduced an error into the tangent differentiated code, inside the tangent derivative of some function called "POLYSURF":


$> exeDD1 | exeDD2
Starting TGT test, epsilon=0.1E-07, zero=0.1E-04, errmax=10.0%
===========================================================
  AT:entry OF                                 MYFUNC
    AT:entry OF                                POLYPERIM
    AT:middle OF                                POLYPERIM
      AT:entry OF                                 INCRSQRT
      AT:exit OF                                 INCRSQRT
      AT:entry OF                                 INCRSQRT
      AT:exit OF                                 INCRSQRT
    AT:exit OF                                POLYPERIM
    AT:entry OF                                POLYPERIM
    AT:middle OF                                POLYPERIM
         ... lots of lines deleted here ... 
    AT:exit OF                                POLYPERIM
  AT:middle OF                                 MYFUNC
    AT:entry OF                                 POLYSURF
    AT:middle OF                                 POLYSURF
pp:   -0.1000000000000000E+01 (ad) 90.0% DIFF WITH (dd) -0.1000000011686097E+02
      AT:entry OF                                 INCRSQRT
pp:    0.3001997501343353E+01 (ad)150.0% DIFF WITH (dd) -0.5998002627904953E+01
      AT:exit OF                                 INCRSQRT
polysurf:    0.3001997501343353E+01 (ad)150.0% DIFF WITH (dd) -0.5998002627904953E+01
    AT:exit OF                                 POLYSURF
y2:    0.3787447771453199E+13 (ad) 92.3% DIFF WITH (dd) 0.2901041015625000E+12
  AT:exit OF                                 MYFUNC
Final result y2: 0.3787447771453199E+13 (ad) 92.34038% DIFF WITH (dd) 0.2901041015625000E+12
===========================================================

From this log, you can deduce that DD and AD derivatives start to diverge between the "middle" point of subroutine POLYSURF and the following call to subroutine INCRSQRT, and the faulty derivative is that of variable pp. The error in the differentiated code is probably nearby. Now you can start to inspect the code from that point, identify the bug, and maybe send us a bug report !

Refining/focusing the test: It is clear what the "entry" and "exit" debug points of a procedure are. They are placed automatically by Tapenade when provided -debugTGT option. The "middle" debug point is also placed automatically by Tapenade -debugTGT option. You can easily find it in the differentiated code. For more accuracy, you can add debug points by placing $AD DEBUG-HERE directives in your original source. For instance (here with F77 syntax for comments. i.e. a "C" in column 1):


         IF (pp.EQ.0) pp=ns
C$AD DEBUG-HERE CP4 cp.eq.4
         dx = X(cp)-X(pp)

defines a new debug point named "CP4". The second argument (optional, default is true) of the directive is a test (with no white space in it, please), and debug point is active only when the test is true. If no test is given, the debug point is always active. There can be a third argument (optional, default is false) that, when true, forces the debug point to be active even if debug of the enclosing procedure is not active (see below). Please note that a debug point directive can be added only before a plain statement such as an assignment, a call, a CONTINUE... Conversely, it cannot be placed before a loop header. If you need to place the debug point before a loop header, place a CONTINUE first, and place the debug point on it.

By default, debugging occurs on every "active" variable at every debug point of every subroutine called. You can control debugging for the complete call tree below a particular subroutine call, by placing the $AD DEBUG-CALL directive in your original source before this particular call. For instance:


C$AD DEBUG-CALL false
       perim = perim+ i*POLYPERIM(X,Y,ns)

turns debugging off for the call tree below this function call. The false can be replaced by something more elaborate (no white space in the test please!). When debugging is turned off inside a particular sub tree of the call tree, no test is made and no message is printed for this sub call tree. However, you have the possibility to force debugging inside this sub call tree by adding a third argument to some $AD DEBUG-HERE or $AD DEBUG-CALL inside. This third argument must be a test. When it evaluates to true, debugging is temporarily turned on again for the debug point or inside the call in question.

CHECK THE REVERSE DERIVATIVES USING THE DOT-PRODUCT TEST:

Mathematical principle: The dot-product test relies on the fact that for every program, procedure, or part P of a procedure, for every vector Xd in the space of the inputs of P and for every vector Yb in the space of the outputs of P, the following scalar:
Yb^* . J_P . Xd (where ^* is transposition and J_P is the Jacobian (derivative matrix) of the function implemented by P) can be computed from left to right or from right to left: (Yb^* . J_P) . Xd = Yb^* . (J_P . Xd) Since (Yb^* . J_P) is in fact Xb^*, the output of the reverse differentiated program P_B applied to Yb, and conversely (J_P . Xd) is in fact Yd, the output of the tangent differentiated program P_D applied to Xd, we find that correct tangent- and reverse-differentiated codes P_D and P_B must be such that: Xb^* . Xd = Yb^* . Yd or in terms of dot-product (Xb . Xd) = (Yb . Yd)

Testing principle: We assume that the tangent-differentiated code is correct, for instance because it was validated by the divided-differences method. We will validate the adjoint program P_B by checking that this dot-product equality holds with the assumed-valid P_D, and locate any part of the reverse differentiated program where the equality doesn't hold.
To this end, we will run simultaneously two instances of the differentiated code, augmented with special debugging calls at selected locations.

The first instance, called "codeBB1", runs P_B on input X.
The second instance, called "codeBB2", runs P_D on input X. Caution, this is not a typo: we really mean the tangent P_D.

Both codeBB1 and codeBB2 compute the above "adjoint-times-tangent" dot-product for each piece of code between each pair of successive run-time locations in the code. Both must obtain the same dot-product results for the same piece of code. More specifically, consider any piece of code PC between two successive run-time locations L1 and L2, calling V1 (resp. V2) the collection of all variables at location L1 (resp. L2).
During the adjoint of PC, codeBB1 first resets V2b to some randomly chosen but reproducible values, then runs the adjoint differentiated code for PC (recall that the adjoint goes backwards from location L2 back to location L1!), and finally computes the dot-product (V1b . V1d) of the obtained V1b with some randomly chosen but reproducible values V1d and somehow sends the dot-product over to codeBB2.
On its side, while running the tangent differentiated code on the same piece of code PC between the corresponding successive run-time locations L1 and L2, codeBB2 first resets V1d to the same randomly chosen values as codeBB1, then runs the tangentdifferentiated code for PC (this time forward from location L1 to location L2), and finally computes the dot-product (V2b . V2d) of the obtained V2d with the same randomly chosen V2b as codeBB1.
Therefore codeBB2 just needs to test for equality up to machine precision between the (V1b . V1d) received from codeBB1 and the locally computed (V2b . V2d), and send a message if the test fails.

Testing process: Suppose again that the "central" part looks like:


          ... whatever code is before ... 
C Beginning of the procedure to differentiate
       CALL MYFUNC(x1, x2,..., y1, y2,...)
C End of the procedure to differentiate
          ... whatever code comes after ...

Define again two copies of your complete code, that will differ only in this "central" part.

The first copy, that we will call "codeBB1", compiles into an executable that we will call "exeBB1". In "codeBB1", instead of calling MYFUNC, you must call its adjoint differentiated version MYFUNC_B, and you must place a few debugging primitives before and after, as follows:


          ... whatever code is before ... 

          Now initialize the REVERSE differentiated variables, e.g.:
          (this step is NOT absolutely necessary for debug !)
       x1b = 0.d0
       DO i=1,ns
         x2b(i) = 0.d0
       ENDDO
       y1b = 1.d0
       DO i=1,20
         y2b(i) = 1.d0
       ENDDO
          ...
          Now prepare for the test:
       CALL DEBUG_BWD_INIT(1.d-5, 0.1d0, 0.87d0)
       CALL DEBUG_BWD_CALL('MYFUNC', .true.)
C Beginning of differentiated part
       CALL MYFUNC_B(x1, x1b, x2, x2b, ..., y1, y1b, y2, y2b, ...)
C End of differentiated part
          Now terminate the test:
       CALL DEBUG_BWD_EXIT()
       CALL DEBUG_BWD_CONCLUDE()

          ... whatever code comes after ...

The second copy, that we will call "codeBB2", compiles into an executable that we will call "exeBB2". In "codeBB2", instead of calling MYFUNC, you must call its tangent differentiated version MYFUNC_D, and you must place a few debugging primitives before and after, as follows:


          ... whatever code is before ... 

          Now initialize the TANGENT differentiated variables, e.g.:
          (this step is NOT absolutely necessary for debug !)
       x1d = 1.d0
       DO i=1,ns
         x2d(i) = 1.d0
       ENDDO
       y1d = 0.d0
       DO i=1,20
         y2d(i) = 0.d0
       ENDDO
          ...
          Now prepare for the test:
       CALL DEBUG_FWD_INIT(1.d-5, 0.1d0, 0.87d0)
       CALL DEBUG_FWD_CALL('MYFUNC')
C Beginning of differentiated part
       call MYFUNC_D(x1, x1d, x2, x2d, ..., y1, y1d, y2, y2d, ...)
C End of differentiated part
          Now terminate the test:
       CALL DEBUG_FWD_EXIT()
       CALL DEBUG_FWD_CONCLUDE()

          ... whatever code comes after ...

A few remarks and explanations:

Each copy "codeBB1" and "codeBB2" will be executed independently. Each must use or read from the same data files as the original code, and should behave exactly the same until reaching the central part. You don't need to duplicate every source file to define these copies "codeBB1" and "codeBB2". You probably need only to duplicate the file that contains the "central" part. The rest should be taken care of by the compilation and link commands.
Note that "codeBB1" makes use of the reverse-differentiated code MYFUNC_B and of the associated differentiated variables x1b etc. The code for MYFUNC_B must be built by Tapenade by reverse differentiation of the source code, with the only additional command-line option -debugADJ.
Conversely, "codeBB2" makes use of the tangent-differentiated code MYFUNC_D and of the associated differentiated variables x1d etc. The code for MYFUNC_D must be built by Tapenade by tangent differentiation of the source code, with the only additional command-line option -debugADJ.
The command lines for the above tangent and reverse differentiation for debugging must have the same options (except of course for the -d versus -b, respectively). In particular they must have the same head procedure, the same independent vars, and the same dependent vars.
Each executable "exeDD1" and "exeDD2" must be linked with the debugging library provided in the "First-Aid Kit". This library consists of file debugAD.f and its include file debugAD.inc
The calls to DEBUG_BWD_INIT or to DEBUG_FWD_INIT must have the same arguments. The first is called "almost-zero" (see below). The second is the "threshold" (see below) error percentage above which a message is printed. The third is the "seed" that influences the random choice of vectors Xd and Yb during testing.
In the prepared code above, notice that debug statements do not concern individual differentiated variables. This is because, unlike the divided-differences test, this dot-product test is global and cannot be applied to a single variable.
Don't forget to declare all differentiated variables in the declaration part of your codes "codeBB1" and "codeBB2".
The new differentiation invocations (Tapenade applied in tangent and reverse modes both with the additional command-line option -debugADJ) may cause additional messages printed, that ask e.g. for the size of array dimensions. These messages must be taken care of, in the way explained in this FAQ: see the section about the particular message.

When "exeBB1" and "exeBB2" are ready, run the divided differences test by just typing the command line:


   $> exeBB1 | exeBB2

using a UNIX pipe "|" (or equivalent). What happens behind the scene is:
exeBB1 calls MYFUNC_B, which is conceptually split into a sequence of code pieces between successive points placed automatically by Tapenade or placed by the user by means of directives. At the beginning of each (reverse differentiated) piece (actually it's what we call its downstream end, because control flow is reversed...), pseudo-random values (using "seed") are assigned to the current reverse differentiated variables V2b by procedure calls such as DEBUG_ADJ_WREAL8. At the end of the same piece (actually it's what we call its upstream end, because control flow is reversed...), the current reverse differentiated variables V1b are multiplied by dot-product with a randomly-filled V1d, through procedure calls such as DEBUG_ADJ_RREAL8. The results are sent into std-out, therefore into the pipe, through procedure calls such as DEBUG_ADJ_RDISPLAY.
In parallel, exeBB2 reads from std-in, therefore from the pipe, and reverses the sequence of incoming dot-products. exeBB2 then calls MYFUNC_D, which is split in a way that matches the splitting of MYFUNC_B. At the beginning of each (tangent differentiated) piece, i.e. at the upstream end of this piece, the same random values are assigned to the current tangent differentiated variables V1d, by procedure calls such as DEBUG_ADJ_WREAL8. At the end of the same piece, i.e. the downstream end of this piece, the current tangent differentiated variables V2d are multiplied by dot-product with the same randomly-filled V2b, through procedure calls such as DEBUG_ADJ_RREAL8. The dot-product is compared with the one coming from exeBB1, by a call to procedure DEBUG_ADJ_RDISPLAY. Those dot-products must be equal. If the two dot-products are almost zero (i.e. absolute value below the given "almost-zero"), no comparison is done. Otherwise, if the percentage of difference is more that the "threshold", a message is printed on the screen, during the summary done by the final call to DEBUG_FWD_CONCLUDE.

Interpreting the test result: What you obtain on the screen looks like what follows. In this example, we introduced an error into the reverse differentiated code, inside the reverse derivative of some function called "POLYSURF":


$> exeBB1 | exeBB2
Starting ADJ test, zero=0.1E-04, errmax=10.0%, random_incr=0.87E+00
===========================================================
  AT:entry OF                                 MYFUNC
    AT:entry OF                                POLYPERIM
    AT:middle OF                                POLYPERIM
         ... lots of lines deleted here ... 
    AT:exit OF                                POLYPERIM
  AT:middle OF                                 MYFUNC
    AT:entry OF                                 POLYSURF
    AT:middle OF                                 POLYSURF
49.0% DIFFERENCE!!  fwd: 0.1156790000000001E+02  bwd: 0.2268820000000001E+02
      AT:entry OF                                 INCRSQRT
      AT:exit OF                                 INCRSQRT
    AT:exit OF                                 POLYSURF
  AT:exit OF                                 MYFUNC
End of ADJ test. 1 error(s) found. WARNING: testing alters derivatives!
===========================================================

The last line of this log just reminds you that the adjoint debug test keeps overwriting derivatives for the purpose of testing. Therefore whatever derivatives it may provide in the end are nonsense and should not be used.

From this log, you can deduce that there is an error in the reverse differentiation of the piece of code between the "middle" point of subroutine POLYSURF and the following call to subroutine INCRSQRT. Now you can start to inspect the code from that point, identify the bug, and why not send us a bug report (thank you!)

Refining/focusing the test: As for the divided-differences test, the "entry" and "exit" debug points are clear enough, and the "middle" debug point is placed arbitrarily by Tapenade. For more accuracy, you can add debug points by placing the same $AD DEBUG-HERE directives in your original source. Remember, place debug points before plain statements, not before a loop header! You can also place $AD DEBUG-CALL directives in your original source to control debugging more finely inside the call tree. Notice however that the third argument of these directives is simply ignored by the dot-product test. In other words, if debugging is turned off for a given sub call tree, there is no way to turn it on locally inside the sub call tree. Notice finally that it is delicate and dangerous to try and add new debug points by hand into the reverse differentiated code. On the other hand, it is rather easy and safe to turn off/on existing debug points inside the reverse differentiated code, without needing to re-differentiate with different $AD DEBUG-**** directives. This may prove handy as running Tapenade on a big code can be long. To do so, you need to edit only the reverse-differentiated code, as follows:

To turn off/on testing inside the call tree below a particular call to procedure FOO, find this call to FOO_B, move upward to the debugging if-then-else before it, to reach the call to CALL DEBUG_BWD_CALL('FOO', "boolean-expression") you may change the boolean second argument at will.
To turn off/on a debug point named "mypoint", use its name to locate the debug point i.e. find the test: IF ("boolean-expression" .AND. DEBUG_BWD_HERE('mypoint')) THEN and change at will the boolean before the .AND.. Debug points named "entry", "exit", "beforeCall", and "afterCall" can not and must not be turned off individually.

PROBLEMATIC INTERACTION WITH INDEPENDENT AND DEPENDENT PARAMETER SETS:

This may cause problems in the tangent validation ("divided differences") because it affects the way derivatives are initialized.
This will certainly cause problems in the adjoint validation ("dot product") if the tangent and adjoint codes are built with (in)dependent paramaters that don't match

either add the command-line option -fixinterface and the Independent and Dependent parameters will not be modified,
or modify by hand your Independent and Dependent parameter sets, according to the variables indicated by the above messages. Then the sets will be coherent again between the tangent and the adjoint codes.

Validation of the differentiated programs (OBSOLETE METHOD)

This section is kept here only for the record. It describes the old method that Tapenade provided before 2011. We now have a simpler, more powerful method, described here.

In any case, to ease our validation mechanism, we strongly advise you to follow a few preparation steps, before you even start to differentiate anything. You will understand the reason for these steps if you go through the validation process that follows.

CHECK THE TANGENT DERIVATIVES WITH RESPECT TO DIVIDED DIFFERENCES:

In the following, words between double quotes and drawn in this color (such as "SHAPE") are indeed templates, that must be instantiated by actual strings depending on the context. Square brackets represent additional arguments, and the star represents repetition.
In the example pieces of programs, actual pieces of code are written in this sort of dark red, short strings in double quotes are "patterns" as above, and

      "entiere lines between double quotes and drawn in the pattern color"

represent a piece of code that you must write at that place.

This is the standard way to test the tangent derivatives. Run your original subroutine P with input X, then with X+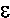*Xd, then compute:

You should get nearly the same result as when running the tangent differentiated subroutine P_d(X,Xd,Y) Differences should be only on a few last decimals.
If this is not the case, here is a way to find where it goes wrong. Use the given library ddTest.f from the AD First-Aid kit. ddTest.f defines subroutines whose name is of the form


       DD"TYPE""SHAPE"("(STRING) variable name",
                 "(FORTRAN TYPE) original variable",
                 "(SAME FORTRAN TYPE) differentiated variable"
                 [,"(INTEGER) array length"])

These procedures compare dynamically (at run-time) the derivatives obtained by divided differences (see below how they are built) with the derivatives obtained normally by the tangent differentiated program. If there is a difference, the procedure prints a message. This test is done each time one of these DD* procedures is encountered, on the variable passed as argument.
Syntax details:

"TYPE" is one of real4, real8, etc
"SHAPE" is ARRAY for an array, and nothing for a scalar.
The first argument is any string (no white space please!) in principle, you should put the name of the variable you are testing. This name is only used to be printed!
The second argument is the original variable that you want to test.
The third argument is its corresponding differentiated variable.
For arrays, an extra argument gives the total size of the array, i.e. the product of the sizes of all dimensions.

For example, if at a given point, you want to test the derivative of the REAL*8 x, just insert the call:

       CALL DDREAL8("x", x, xd)

To test a whole array, e.g. REAL T(10,0:2), and REAL means REAL*4 on your system

       CALL DDREAL4ARRAY("T", t, td, 30)

You may test only one cell of an array, and then you don't need the dimension:

       CALL DDREAL4("T_3_2", t(3,2), td(3,2))

You may even cheat a little with array sizes, to check only a fragment of it:

       CALL DDREAL4ARRAY("somepartofT", t(3,1), td(3,1), 5)

Notice that these calls must be inserted in the code after the traced variable and its derivative have been computed, and before the traced variable or its derivative get overwritten later on.

Of course, the above works only on a prepared program. Here is how to prepare it: We assume you have been differentiating a subroutine F. Then the file that uses F_D probably has the shape:


       "set all inputs x1, x2, ... to their initial values"
       "set the differentiation tangent direction in x1d, x2d,..."
       CALL F_D(x1, x1d, x2, x2d,..., y1, y1d, y2, y2d,...)
       "use the resulting derivatives y1d, y2d, ..."

Caution: By "inputs" (resp. "outputs") of F, we mean logical inputs (resp. outputs), i.e. all values that will be used inside (resp. returned by) F. This comprises not only the arguments, but any common, global, etc... of any sort that holds a value that is used inside (resp. returned by) F. Since this verification mechanism needs to perform two runs of F_D on the same inputs, you will need to store all these inputs (we call this "taking a snapshot") before the first run of F_D, and restore them before the second run. If you know your code very well and you are certain that some inputs are never modified between the 1st and the 2nd run of F_D, then you may omit them from the snapshot.

You should prepare the above call site so that it now looks like:


       real*8 ddeps, epszero
       integer ddphase, ddfile
       common /DDTESTCOMMON/ ddphase, ddfile, ddeps, epszero

       "set the inputs x1, x2, ... to their initial values"
       "take a snapshot "S" of the initial values of x1, x2,..."
       "set the differentiation tangent direction in variables x1d, x2d,..."
       "take a snapshot "SD" of this initial direction x1d, x2d,..."
       ddeps = 1.d-5
       "set the inputs x1, x2, ... to a value "plus ""
       x1 = x1 + ddeps*x1d
       ...
       epszero = 0.00000001
       ddphase = 1
       ddfile = 37
       OPEN(37, FILE='epsvalues')
       CALL F_D(x1, x1d, x2, x2d,..., y1, y1d, y2, y2d,...)
       CLOSE(37)
       "reset the inputs x1, x2, ... to their initial values, using "S""
       "reset the differentiation tangent direction in x1d, x2d,...using "SD""
       ddphase = 2
       OPEN(37, FILE='epsvalues')
       CALL F_D(x1, x1d, x2, x2d,..., y1, y1d, y2, y2d,...)
       CLOSE(37)

This program will encounter all the DD* calls that are present in F_D. On the first sweep (ddphase=1), it will just store the current value of the variable, which is the value "with

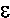" into a temporary file epsvalues. If this file really grows too big, you might consider modifying the present strategy, for example building two separate processes that communicate through a UNIX pipe. On the second sweep (ddphase=2), the value "with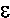

" is retrieved, and combined with the current value to build the "divided differences" derivative. This derivative is in turn compared with the AD analytic derivative. if the divided difference is far from the AD derivative (this is parametrized inside ddTest.f, where the percentage of difference is in variable diff), then the word "DIFFERENCE" is printed on the standard output close to the faulty derivatives. Please note that nothing is printed when both derivatives (DD and AD) are zero. Tapenade has an option that places automatically the calls to all necessary DD* procedures, at the beginning and end of user-specified procedures. This is of course an option of the tangent mode of AD and its syntax is:


   $> tapenade -d -traceactivevars "units" ...

The following does it on all units:


   $> tapenade -d -traceactivevars %all% ...

Of course, you may add extra DD* trace calls by hand after that.
Then playing with adding/moving calls to DD* procedures, you will hopefully close in to the place where the F_D file is incorrect!

CHECK THE REVERSE DERIVATIVES USING THE DOT-PRODUCT TEST:

      "entiere lines between double quotes and drawn in the pattern color"

represent a piece of code that you must write at that place.

The dot-product test assumes that, if you call J the jacobian of F, and Jt its transpose, F_D(X,Xd) computes actually Yd = J.Xd and F_B(X,Yb) computes actually Xb = Jt.Yb Therefore, for a given Xd, F_D returns Yd = J.Xd, and if we set Yb=Yd F_B(X,Yb) then returns Xb = Jt.J.Xd We observe that if the program is correct, then the dot product
(Xb | Xd) == (Jt.J.Xd | Xd)
should be equal to
(J.Xd | J.Xd) == (Yd | Yd)

Tapenade will automatically place the necessary calls inside the differentiated code for you. Use the option -dptest provided in the differentiation command. Logically, you should first try to validate the complete differentiated program, whose root is here procedure F. Also, the dot-product test requires a preliminary run of a tangent differentiated code, so you should use Tapenade to generate both a tangent and a reverse differentiated code, both being aware of the dot-product test on F through the -dptest option. Finally, the -dptest option is incompatible with the -traceactivevars option used to validate the tangent mode, so make sure not to use it now. All in all, you should produce validation codes for F_D and F_B with commands:


   $> tapenade -d -head F -dptest "F" ...
   $> tapenade -b -head F -dptest "F" ...

Look out for (AD14) messages such as: (AD14) Cannot instrument hidden active variable VVV . These tell you that the preparation of the code for the dot-product test could not be completed, because the test needs to maipulate variable VVV which is a global not visible by F. To solve this, you need to make this variable visible inside F, and differentiate again.

Then, to run the dot-product test, you must also prepare your calling program as follows:


       INTEGER dpunitcallcount,dptriggercount
       COMMON /DPCALLCOUNT/dpunitcallcount,dptriggercount

       "set the inputs x1, x2, ... to their initial values"
       "take a snapshot "S" of the initial values of x1, x2,..."
       "set the differentiation tangent direction in x1d, x2d,..."
       dptriggercount = 1
       CALL F_D(x1, x1d, x2, x2d,..., y1, y1d, y2, y2d,...)
       "reset the inputs x1, x2, ... to their initial values, using "S""
       "assign the y1d, y2d, ... into y1b, y2b,..."
       CALL F_B(x1, x1b, x2, x2b,..., y1, y1b, y2, y2b,...)
       CALL DPPRINTSUMMARY()

Be careful to check that the call patterns of the F_D and F_B subroutines match exactly their definition, which you will find in the differentiated files. In fact, using the -dptest option might change the number of arguments of these differentiated subroutines, so it is important to check that definitions and call match.

Here starts the "Compile-and-Run" step, to which we will cycle later in this explanation...
Compile the test code and link it with the two libraries specific to the dot-product test, dptest.f and dpStack.c. Since this uses the reverse mode, it should also be linked with the usual adStack.c. All these files are provided in the AD First-Aid kit.

Running the test code will print on the standard output the values of the dot-products for each fragment between the milestone points placed in the code, printing the products (Yd | Yd) when going forward, and the products (Xd | Xb) when going backward. There is a summary printed at the end of the process by the call to DPPRINTSUMMARY() in the test site, which should make it easier to read. If there is no bug, corresponding forward and backward dot-products should return the same value, and the validation process is complete. If this is not the case, assuming that you have validated the tangent mode as indicated above, this shows there is a problem with the reverse mode of the fragments for which the dot-products differ.

Then the question is: where does the problem occur? To find this out, we propose that you use a divide and conquer method, by moving or adding extra milestones for the dot-product test. For example the -dptest "F" has set only the minimal two milestones, at the entry and at the exit of F, plus one "somewhere in the middle". These milestones appear in the summary with default names: EntryIntof, Inf, and ExitFromf respectively. Choose one (or more...) points in (the control flow of) subroutine F_D. Find the EXACTLY corresponding point in the reverse sweep of subroutine F_B. Then move the piece of code that defines the Inf milestone of F_D (it is an in-then-endif statement controlled by IF (DPFWDTESTCOUNT('f')) THEN) to the chosen new point in F_D. Alternatively you may duplicate this code (give it a new name e.g 'PointAInf') to place an additional milestone. Do the same for F_B. Don't call Tapenade again at this step, because it would overwrite your hand-modified F_D and F_B codes. Compile and run the test again as explained above, from this "Compile-and-Run" step.

If the faulty zone eventually gets reduced to a handful of simple statements, then you should be able to find the bug. Otherwise the faulty zone may be reduced to a single call to a procedure called, say, G. You must now restart the divide and conquer process this time on G. Use Tapenade to place the necessary dot-product calls, with the -dptest option.


   $> tapenade -d -head F -dptest "G" ...
   $> tapenade -b -head F -dptest "G" ...

Look out for (AD14) messages again!
Also, the bug may appear not on the first run-time call to G, but on some later call, for instance the 12^th. In this case, replace


       dptriggercount = 1

in the calling toplevel by


       dptriggercount = 12

then resume from the "Compile-and-Run" step.

We advise you not to create new milestones by hand, except by copy-paste as explained above, because this is rather delicate. The order of PUSH and POP's matters, and it is extremely important that no active variable goes through a milestone without being caught by one PUSH/POP. This dot-product validation process is much more fragile than the divided differences validation of the tangent derivatives.

Lastly, when all goes well, don't forget to remove the validation options from your differentiation command lines!

All Warning or Error messages :

What do all these Warning and Error messages mean?

TAPENADE issues a number of messages resulting from the preliminary analyses done before actual differentiation. Although the temptation is strong, these messages should not be ignored right away. Especially when AD is concerned, these messages can be the indication that the program runs into one limitation of the AD technology. So even if the original program compiles and runs correctly with your compiler, these messages warn you that differntiation may produce a faulty program.

Some messages are requests for help: when TAPENADE needs some help from the user, e.g. because it needs and does not know the size of an array, it issues a message that asks you to give this size after differentiation is done. Otherwise the resulting program will not run.

Here is the list of all Warning and Error messages of Tapenade, grouped by category, and pointing to a discussion on their meaning and importance. This list may not be up to date, unfortunately...

Declarations messages
DD01,DD02,DD03,DD04,DD05,DD06, DD07,DD08,DD09,DD10,DD11,DD12, DD13
Type messages
TC01,TC02,TC03,TC04, TC05,TC06,TC07,TC08,TC09, TC10,TC11,TC12,TC13,TC14, TC15,TC16,TC17,TC18,TC19, TC20,TC21,TC22,TC23,TC24, TC25,TC26,TC27,TC28,TC29, TC30,TC31,TC32,TC33,TC34, TC35,TC36,TC37,TC38, TC40,TC41,TC42, TC50,TC51,TC52
Control flow messages
CF01,CF02,CF03,CF04,CF05
Data flow messages
DF01,DF02,DF03,DF04
Automatic Differentiation messages
AD01,AD02,AD03,AD04,AD05, AD06,AD07,AD08,AD09,AD10, AD11,AD12,AD13,AD14,AD15, AD16,AD17,AD18,AD19,AD20, AD21

Declarations problems:

(DD01)	Cannot combine successive declarations of variable var: Type1 and Type2 (ignored new)
(DD02)	Cannot combine successive declarations of character array: Type1 and Type2 (ignored new)
(DD03)	Cannot combine successive declarations of constant const type: Type1 and Type2 (ignored new)
(DD04)	Double definition of function Func (ignored new)
(DD05)	Cannot combine successive declarations of function Func (ignored new)
(DD06)	Cannot combine successive declarations of function Func return type: Type1 and Type2 (overwritten previous)
(DD07)	Cannot combine successive declarations of function Func kind: kind1 and kind2 (ignored new)
(DD08)	Double declaration of external function Func
(DD09)	Double declaration of intrinsic function Func
(DD10)	Double declaration of the main program: Func1 and Func2 (overwritten previous)
(DD11)	Double declaration of function Func in library file LibraryFile
(DD12)	Cannot combine successive declarations of type Type (ignored new)
(DD13)	Double definition of label label (ignored new)

There are two successive definitions or partial declarations of some symbol, as a variable, constant, type, label or function name. These successive declarations occur in the same scope and do not combine into a coherent declaration for the symbol. TAPENADE therefore chooses either to ignore the new piece of declaration, or to overwrite the previous piece of declaration, as indicated by the message. For DD08 and DD09, the two choices are equivalent.

Why should you care? TAPENADE chooses to ignore the indicated declaration or part of your original program. Therefore the types considered by TAPENADE may not be the ones you expect, or the program actually differentiated may differ from the program you think. In particular when types are concerned, remember that differentiation occurs only on REAL (or COMPLEX) typed variables. Therefore some variable may have no derivative whereas you think it should have one. Also for DD13 or DD10, the flow of control may be different from what you think, or from what your local compiler used to build. Also for DD11, some information that you give about an external function may be ignored and replaced by another one.

What can you do? Remove the declaration or definition in excess, or modify conflicting declarations so that they combine well into the type that you expect. For DD11, clean up the library file by merging the data about a given function into one single entry.

Type problems:

(TC01)	Expression is expected to be numeric, and is here Type
(TC02)	Expression is expected to be boolean, and is here Type
(TC03)	Expression is expected to be a record, and is here Type
(TC04)	Expression is expected to be a pointer, and is here Type
(TC05)	Expression var is expected to be an array, and is here Type
(TC06)	Loop index is expected to be integer, and is here Type
(TC07)	Loop bound is expected to be integer, and is here Type
(TC08)	Loop times expression is expected to be integer, and is here Type
(TC09)	Real part of complex constructor is expected to be numeric, and is here Type
(TC10)	Imaginary part of complex constructor is expected to be numeric, and is here Type
(TC11)	Argument of arithmetic operator is expected to be numeric, and is here Type
(TC12)	Array index is expected to be numeric, and is here Type
(TC13)	Triplet element is expected to be numeric, and is here Type
(TC14)	Substring index is expected to be numeric, and is here Type
(TC15)	Argument of logical operator is expected to be boolean, and is here Type

The indicated expression is used in a context which requires some type. Using the available declarations, the type-checker found that this expression actually has a different type, indicated in the message.

Why should you care? This may be the sign of an error in the program. Even if this original program actually compiles and runs well, remember that differentiation occurs only on REAL (or COMPLEX) typed variables. If some sub-expression becomes of another type, there will be no derivative associated, even if you think there should be one. Remember also that these problems make the program non-portable.

What can you do? Check the types. You may also use the appropriate conversion functions. Be aware that when you convert a REAL into an INTEGER, the differentials are reset to zero.

(TC16)	Type mismatch in assignment: Type1 receives Type2
(TC17)	Type mismatch in case: Type1 compared to Type2
(TC18)	Type mismatch in comparison: Type1 compared to Type2

The two terms in the assignment or comparison, or the switch and case expressions, must have compatible types. Otherwise, the meaning of the instruction is not well defined, and not portable.

Why should you care? This can be the indication for a standard type error and, like above, this can lose derivatives.

What can you do? Check the types. Use conversion functions when appropriate.

(TC19)

Equality test on reals is not reliable

Equality and non-equality are not well defined between REAL's, because they are defined only up to a given "machine precision". Equality test can yield different results on different machines.

Why should you care? As far as AD is concerned, equality tests on REAL's are sometimes used as the stopping criterion for some iterative process. Then it relates to a well-known problem: do the derivatives converge when the function does, and if yes, do they converge at the same speed?

What can you do? Check that this does not impact differentiation. Take care to perform the usual validation tests on the computed derivatives.

(TC20)	Variable var is not declared
(TC21)	No implicit rule available to complete the declaration of variable var
(TC22)	Variable var, declared implicitly as Type1, is used as Type2
(TC23)	Symbol var, formerly used as a variable, now used for another object
(TC24)	Wrong number of dimensions for array Array: n2 expected, and n1 given
(TC25)	Dimensions mismatch in vector expression, Type1 combined with Type2
(TC26)	Incorrect equivalence
(TC27)	End of common /COMMON/ reached before variable var
(TC28)	Variable var cannot be added to common /COMMON1/ because it is already in common /COMMON2/
(TC29)	Common /COMMON1/ declared with two different sizes: s1 vs s2
(TC30)	Type mismatch in argument Arg of function Func, expects Type1, receives Type2
(TC31)	Type mismatch in argument Arg of function Func, declared Type1, previously given Type2
(TC32)	Wrong number of arguments calling Func: n2 expected, and n1 given

These messages indicate conflicts between declaration and usage of some variable. Message TC25 occurs in the context of vectorized programs. Messages TC26 to TC29 indicate a problem in EQUIVALENCE's and COMMON's. Recall that variables in a COMMON are stored contiguously, so that their relative order cannot be changed, and extra variables cannot be inserted occasionaly. Also a variable cannot be in two different COMMON's, and one cannot set an EQUIVALENCE between two variables that already have their own, different, memory space allocated. Messages TC30 to TC32 indicate a mismatch between the formal and actual parameters of a function. Recall that the standards require that formal and actual parameters match in number and size.

Why should you care? In general, if you let the system choose the type of a variable, you run the risk that it becomes REAL while you don't want, or the other way round. And this in turn impacts differentiation. Messages TC24, and TC26 to TC32 are even more serious: They can indicate that the code relies on FORTRAN weak typing to perform hidden equivalence's between two arrays, or to resize, reshape, or split an array into pieces. Since TAPENADE cannot possibly understand what is intended, it might not propagate differentiability and derivatives from the old array shape to the new array shape.

What can you do? Declare variables explicitly. Try to avoid the "implicit" declaration facility. Declare arrays with their actual size (not "1"). Never resize, reshape, or split arrays implicitly through parameter passing, and avoid to do so across COMMON's

(TC33)	Intrinsic function Func is not declared
(TC34)	External function Func is not declared

These messages indicate that you did not provide TAPENADE with the sources of the indicated procedures.

Why should you care? If TAPENADE doesn't see the source of a called procedure, it is obliged to make several worst-case assumptions about it. Moreover, it this procedure must be differentiated, TAPENADE can't do it. You will have to do it yourself. In some cases this can be profitable because an expert user can do a better job than TAPENADE.

What can you do? If you just forgot the procedure's source file, add it to the list of source files. If the procedure is missing for a good reason, first give TAPENADE type and data-flow information about the missing procedures, using either a dummy source procedure, or using our library mechanism. This can only make things better, as the conservative worst-case assumptions often have a negative impact. Then think about these missing procedures: if it turns out they will have a derivative, you will have to provide this derivative: message AD09 will remind you of that later. In the best situation, you are able to write an analytic differentiated code yourself. In the worst situation, you may use divided differences for the derivative of this unknown procedure, but this will loose some accuracy!

(TC35)	Subroutine Func used as a function
(TC36)	Type function Func used as a subroutine
(TC37)	Return type of Func set by implicit rule to Type

These messages indicate conflicts between declaration and usage of some function. Programs with messages TC35 and TC36 should not compile.

Why should you care? In general, if you let the system choose the return type of a function, you run the risk that it becomes REAL while you don't want, or the other way round. And this in turn impacts differentiation.

What can you do? Insert the correct declaration.

(TC38)

Recursivity: Func1-->Func2-->...-->FuncN

Recursivity is when a subroutine Func1 calls a subroutine Func2, which itself calls a subroutine Func3, and so on, and when this eventually leads to calling Func1 again. In other words this is a cycle in the call graph. Basically, this is not an error, although FORTRAN77 used to forbid recursive programs.

Why should you care? It is just a matter of time. Recursive programs are harder to analyze. We are progressively updating TAPENADE analyses so that they cope with recursivity.

What can you do? In the meantime, check that the resulting derivatives are correct, using the classical tests.

(TC40)	No field named name in Type
(TC41)	Recursive type definition

These are illegal uses of types. TC40 says the program looks for a field name which does not exist, and TC41 that some types directly contains a field of the same type, thus yielding an infinite size!

Why should you care? It is surprising is the original program actually compiles! Differentiation is undefined.

What can you do? Rewrite the definitions of these types.

(TC42)

Definition of type Type comes a little too late

The definition of the type came after it was used. This is just a warning, because TAPENADE will do as if the definition was done in due time. But you should better fix this.

(TC50)	Label label is not defined
(TC51)	Label variable var must be written by an ASSIGN-TO construct
(TC52)	Variable var used in assigned-GOTO is not a label variable

These are illegal uses of labels, or label variables.

Why should you care? If labels are misunderstood, the final flow of control that TAPENADE understands and regenerates might not be the one you expect. Therefore TAPENADE does not differentiate the program you expect.

What can you do? Define the labels you use. Use the correct constructs to manipulate label variables.

Control flow problems:

(CF01)	Irreducible entry into loop
(CF02)	Computed-GOTO without legal destinations list
(CF03)	This assigned-GOTO to var goes nowhere
(CF04)	This assigned-GOTO to var only goes to label label
(CF05)	This assigned-GOTO to var is possibly undefined

These messages indicate problems in the flow of control of the program. Message CF01 comes from jumps that go from outside to inside a loop, without going through the loop control header. The meaning of this is not well defined and is probably implementation dependent.

Why should you care? Of course a bad control of a program yields a bad control of its differentiated programs.

What can you do? Avoid irreducible loops. Avoid jumps into loops and into branches of a conditional structure. Try to use structured programming instead. If an assigned-GOTO goes to only one place, at least replace it by a GOTO.

Data flow problems:

(DF01)	Illegal non-reference value for output argument Arg of function Func
(DF02)	Potential aliasing in calling function Func, between arguments arguments
(DF03)	Variable var is used before initialized
(DF04)	Variable var may be used before initialized

These problems are detected through the built-in interprocedural data-flow analysis of TAPENADE.

Why should you care? Programs with DF01 usually provoke segmentation faults. Aliasing (DF02) is a major source of errors for DIfferentiation in the reverse mode, as described in more detail in the "Aliasing" section. Uninitialized variables lead to uninitialized derivatives.

What can you do? Output formal arguments of a subroutine must be passed reference (i.e. writable) actual arguments. It is better to avoid aliasing. When aliasing is really a problem, one can easily avoid it by introducing temporary variables, so that memory locations of the parameters do not overlap. Variables should be initialized before they are used.

Automatic Differentiation problems:

(AD01)	Actual argument Arg of Func is varied while formal argument is non-differentiable
(AD02)	Actual output Arg of Func is useful while formal result is non-differentiable

These two messages are usually associated. They indicate the following situation: Some programs implicitly convert REAL's to INTEGER's during a function call, then these INTEGERS follow their way through the code, and finally are converted back into REAL's during another function call.

Why should you care? If the original REAL's are varied, i.e. depend on the independent input variables, and the final REAL's are useful, i.e. influence the dependent output variables, then this temporary conversion into INTEGER's has lost differentiability and derivatives. Differentiability is lost, derivatives are wrong!

What can you do? If you are sure that these passive recipients that receive a varied variable (AD01) will never be passed later to useful variables, and vice versa that the passive value given to these useful variables (AD02) never originates from a varied variable, then you need not do anything. Otherwise modify the source code: REAL's must remain REAL's! If absolutely necessary, there is a "secret" option in TAPENADE to actually differentiate these strange REAL-INTEGER's...

(AD03)	Varied variable var written by I-O to file file
(AD04)	Useful variable var read by I-O from file file

This is comparable to the above AD01 and AD02. These two messages are usually associated or, to put it differently, if the two messages occur for the same differentiation session, then there is a risk. The risk occurs in the following situation: Some programs write intermediate REAL values into a file and later on, read back these REAL values from this file. This process looses differentiability.

Why should you care? If the written value is varied, i.e. depends on the independent input variables, and the corresponding (equal) value read is useful, i.e. influences the dependent output variables, then this temporary storage into a file has lost differentiability and derivatives. Differentiability is lost, derivatives are wrong!
For instance if the code looks like:


      subroutine TOP(x,y,fileno)
      real x,y,tmp
      integer fileno
      write(fileno,*) x
      ...
      read(fileno,*) tmp
      y = 2.0*x + tmp
      end

Tapenade cannot find the dependency path that goes from the input x through de file "fileno" and finally to the output y. if xd is 1.0 yd will be 2.0, whereas the correct answer should be 3.0.

What can you do? If you are sure that these files that receive varied variables (AD03) will never be read later to write into useful variables, and vice versa that the values read into these useful variables (AD02) never originate from a varied variable, then you need not do anything. Otherwise modify the source code so as not to use files as temporary storage. Use arrays instead. You may also use TAPENADE "Black-box" mechanism to disconnect differentiation on the calling subroutines, and differentiate them by hand, with an ad-hoc mechanism to propagate derivatives.

(AD05)

Active variable var overwritten by I-O

This reminds you that a variable that was active has been overwritten by an I-O operation

Why should you care? The derivative is of course reset to zero. Maybe this is not what you expected?

What can you do? Check that it is OK. Otherwise modify the source so as to put all I-O operations outside the part of the program you are actually differentiating.

(AD06)

Differentiation root procedures Procedure-names have no active input nor output

Tapenade could not find any differentiable influence from the independents to the dependents arguments of procedures Procedure-names

Why should you care? Differentiation is of course impossible for these procedures

What can you do? Either there was an mistake/misspell in the procedure names or variable names given in the command-line arguments -root, -vars, or -outvars. Or there is really no differentiable dependency, i.e. the derivatives are all always zero. Or else there is a dependency that Tapenade could not find => please report bug ?

(AD15)

Irreducible exits from the same scope in procedure Procedure

The control-flow of Procedure has several different ways of leaving some local declaration scope.

Why should you care? In reverse mode, the scope must be re-entered back through each of these ways. The problem is that one cannot repeat the local variables declarations at each of these "backwards-entry" points.

What can you do? Slightly modify the source code, so that the control-flow exits this scope through a unique "last instruction in scope".

(AD16)

Could not find type for temporary variable tempVar to hold expression, please check

Tapenade had to split a long expression, introducing a temporary variable tempVar to precompute the sub-expression expression. The problem is that it was not able to guess the type for the declaration of tempVar.

Why should you care? The differentiated code is wrong. It probably features an unknowntype declaration somewhere, and it will not compile.

What can you do? Modify the source code to perform this expression splitting by hand, so that differentiation need not do it.

(AD17)

Type mismatch in argument n of procedure Procedure, was Type1, is here Type2, please check initialization after diff call

There is a type mismatch on argument n of procedure Procedure, before actual argument and formal argument. It turns out that Tapenade has to reinitialize the argument (or its derivative), after the procedure call. The type mismatch prevents it to do so.

Why should you care? A missing initialization can make all derivatives wrong.

What can you do? Check declarations of actual and formal arguments. If they don't match, modify the source code so that they match. The problem may also arise when the actual argument was split into a temporary variable and the type for this temporary is unknown or wrong. Then maybe modify the source code to perform this splitting by hand.

(AD18)	Inconsistent checkpoints nesting here
(AD18)	Cannot enter into checkpoint twice!
(AD18)	Cannot exit from checkpoint twice!
(AD18)	Checkpoint not closed in enclosing level

These messages indicate that you have used the directives $AD CHECKPOINT-START and $AD CHECKPOINT-END to insert checkpoint in the middle of some procedure's code. The problem is that there directives delimitate code fragments that are not well nested. Either there is a way to jump into a checkpoint without going through a $AD CHECKPOINT-START, or outside a checkpoint without going through a $AD CHECKPOINT-END. See details here.

Why should you care? Your refined checkpointing scheme will not work

What can you do? Check the nesting, adding or removing directives if necessary. Remember that these directives cannot be attached to some control statements. In case of doubt, insert a no-op statement e.g. CONTINUE and attach the directive to it.

(AD19)

Cannot use binomial checkpointing here

For some reason, tapenade doesn't accept binomial checkpointing on the loop where you requested it through directive $AD BINOMIAL-CKP

Why should you care? Ordinary checkpointing will be applied instead

What can you do? See binomial checkpointing for details.

(AD20)

Cannot use II-LOOP directive here

For some reason, tapenade doesn't accept II-LOOP checkpointing on the loop where you requested it through directive $AD II-LOOP

Why should you care? Ordinary checkpointing will be applied instead

What can you do? See loops with independent iterations for details.

(AD21)	End-fragment directive missing in Procedure
(AD21)	Start-fragment directive missing in Procedure

Tapenade has found directives in the source of the said Procedure, that should designate a fragment of the code. For instance the fragment between a $AD DO-NOT-DIFF and a $AD END-DO-NOT-DIFF. Such a fragment must have a unique entry point (the first instruction after entering the fragment) and a unique exit point (the first instruction after exiting the fragment). For some reason, it seems Tapenade has found either an alternative way to enter the fragment, without going through its entry point, or an alternative way to leave the fragment without going through its exit point. This makes the fragment designation ambiguous.

Why should you care? The special treatment that you intended for this fragment will not occur.

What can you do? Check the location of the directives, and the correct nesting of the fragments. Move the directives so that the fragments are properly nested and have each a unique entry and a unique exit. Remember that these directives cannot be attached to some control statements. In case of doubt, insert a no-op statement e.g. CONTINUE and attach the directive to it.

(AD07)

Data-Flow recovery (TBR) on this call to Procedure
Data-Flow recovery (TBR) on this I-O call
Checkpointing this call to Procedure
Checkpointing this piece of code
Binomial checkpointing of this piece of code

needs to save

a hidden variable: extern-var
an undeclared side-effect variable: extern-var
the I-O state

(AD07)

Summary: differentiated procedure of Procedure needs to save undeclared side-effect variables External-Vars from Units

These messages all indicate that the checkpointing mechanism is not certain that it can do a correct job. Checkpointing and TBR are two mechanisms of the reverse mode of AD that rely on saving the current value of some variables, onto a stack, and on restoring them later. Checkpointing may occur at procedure call sites (by default) or at places designated by the end-user through directives (see inline checkpointing, binomial checkpointing, loops with independent iterations). Checkpointing a call to Proc2 inside Proc1 means that the reverse differentiated subroutine of Proc1 is going to call Proc2 twice, or more precisely the original Proc2 once and then the differentiated Proc2. Roughly speaking, these two calls must be made with the same inputs, so that the 2nd call is an exact duplication of the 1st call. To do this, a minimal "environment" needs to be stored just before the 1st call to Proc2 and restored just before the 2nd call. We know how to save and restore most variables, e.g. the formal parameters of Proc2, but also the globals known by Proc1 and Proc2. cf a quick description of checkpointing, or Tapenade User's guide for something more technical. When the variable that must be saved and restored is not declared at the current location, or is the I-O state, or is hidden for some reason, then this storage is impossible and adjoint differentiation cannot work properly.
Similarly the TBR mechanism stores selected variables just before they are overwritten by any given instruction. Therefore, the TBR mechanism may also run into the same trouble when the overwritten variable cannot be saved at the current location, while being overwritten inside the coming instruction which is a subroutine call or an I-O call. Also notice that Tapenade may incorrectly save/restore pointers to dynamically allocated memory.

Why should you care? The adjoint derivatives may be wrong. Here's an example. Suppose you want to differentiate, in reverse mode, the procedure TOP from this Fortran90 example:


module M
  real :: vm
end module M

subroutine top(X,Y)
  real :: X,Y
  open(20)
  X = X*X
  call foo(X,Y)
  Y = Y*Y
  close(20)
end subroutine top

subroutine foo(X,Y)
  use M
  real :: X,Y
  real :: vc
  common /cc/ vc
  real :: vf
  read (20,*) vf
  vm = vm * vc
  vc = vc * vm
  Y = Y + X*vc + vm*vf
end subroutine foo

Tapenade issues the messages:


top: (AD07) Checkpointing this this call to foo needs to save an undeclared side-effect variable: (global)vm
top: (AD07) Checkpointing this this call to foo needs to save an undeclared side-effect variable: /cc/[0,4[
top: (AD07) Data-Flow recovery (TBR) on this call to foo needs to save the I-O state
top: (AD07) Summary: differentiated procedure of top needs to save undeclared side-effect variables vc, from COMMON /cc/
top: (AD07) Summary: differentiated procedure of top needs to save undeclared side-effect variables vm, from MODULE m

If you look at the differentiated code, you can see that these messages point at serious problems. Considering each of these 5 messages in order:

Variable vm, from module M is effectively modified by the call to FOO_CB in TOP_B. However its original value will be needed by the coming call to FOO_B. Thererefore, TOP_B must do something to save and restore this original value. The problem is that TOP_B doesn't even know about vm because it doesn't USE the module M.
The same holds for variable vc, from common /cc/.
lastly, FOO reads the value of variable vf, from the file with file-id 20. However, the checkpointing mechanism duplicates this reading, and therefore the value of vf that will be used in FOO_B will be wrong.
The 4th message here is a summary all the previous messages regarding variable vc, because there may have been many if there are many subroutine calls.
Similarly, the 5th message is the summary about vm..

What can you do? Either make absolutely sure that this is not a problem in the present case, because you know that the second call to Proc2 will behave just like the 1st one, at least as far as differentiation is concerned. You need to know the code for that because errors will be hard to track down. For instance, one favorable situation is when the (AD07) message corresponds only to prints of messages on the screen or into a log file. The messages will appear twice, but derivatives should be correct.
Or modify your code so that the problem disappears, for instance insert the COMMON declaration at the level of the calling subroutine. or transform the SAVE variables into elements of a COMMON that everyone can see, or add the needed USE declarations, or take the file I/O or dynamic memory allocation or deallocation outside the code to differentiate, Use the Summary message that gives you a condensed list of the variables declarations missing in each procedure.
Or (more high-tech!) When the message mentions the checkpointing cause, deactivate the checkpoint in question. You may tell Tapenade not to checkpoint the calls that raise the problem using the "nocheckpoint" directive.

(AD08)	Differentiated procedure of Procedure needs to initialize to 0 a hidden variable
(AD14)	Summary: differentiated procedure of Procedure needs to instrument undeclared side-effect variables External-Vars from Units.

These messages are very similar to the (AD07) series. They indicate that either an initialization or the Tapenade debugging mechanism need to have access to a hidden variable.

Why should you care? The differentiated code is wrong.

What can you do? Modify the source code to make the necessary variables visible at the locations indicated by the messages.

(AD09)

Please provide a differential of function Func for arguments arguments

You must provide the differentiated program with a new function, differentiated from Func with respect to the input and output parameters of Func specified in the arguments. Probably Func is an external function, for which TAPENADE has no source, and therefore it couldn't differentiate it.

Why should you care? If you don't give this new function, the differentiated program will probably not compile.

What can you do? Define this new function. You have the choice of the method. Maybe you know explicitly the derivative mathematical function, which can be implemented efficiently. Maybe you have the source and you may use AD again, with TAPENADE or with another tool. Maybe you just want to run a local "divided differences" method, knowing that this might slightly degrade the precision of the derivatives. In any case, make sure that you provide a differentiated function in the correct mode (tangent, reverse...), and which adheres to the conventions of TAPENADE about the name of the function and the order of its parameters.

(AD10) User help requested: constant NBDirsMax must hold the maximum number of differentiation directions

In vector (i.e. multi-directional) modes, differentiated variables receive an extra dimension to hold the values for each differentiation direction followed simultaneously. Declaration of the differentiated variables must declare the size of this dimension. Tapenade lets you specify this size through the integer variable NBDirsMax.

Why should you care? If you don't give this size, the "vector-" differentiated program will not compile.

What can you do? Declare and initialize this variable in a separate file, in the fashion described for message (AD11).

(AD12) User help requested: unknown dimension n of array Array

(AD11) User help requested: constant name must hold the size of dimensionn of Array (should be Hint)

Messages (AD12) and (AD11) usually come together. In some cases, for example in reverse-mode AD, the differentiated code needs the size of dimensions of arrays. This happens for instance when saving/restoring array values, or when declaring or initializing derivative arrays, or when passing arrays to the specialized procedures that manage Tapenade's debugging mode. In some cases this size is unknown. In other cases this size is known, but is dynamic and therefore cannot be used in a Fortran77 declaration.

Why should you care? If you don't give this size, the differentiated program will not compile.

What can you do? Follow the messages (AD11) to find the (rather long) names that Tapenade has created and used in the differentiated code where the size was needed. Declare and define these variables in a separate file that you will keep on the side, and that will be linked to the differentiated code at compile time. Depending on the application language, this may be done through an include file, or in the Fortran90 module DIFFSIZES.
Alternatively,in Fortran90, you can use the command-line option -noisize, that will tell Tapenade to replace this mechanism (new variables containing the sizes) by dynamic calls to the Fortran90 SIZE primitive.
Note that doing this will not suppress the messages, as the source code is not modified. You can also explicit this size in the declarations of the original source code, so that tapenade finds it statically, and the messages will go away!

(AD12)	User help requested: unknown dimension n of array Array
(AD11)	User help requested: constant name must hold the size of dimensionn of Array (should be Hint)

Frequently Asked Questions on Tapenade¶

Problems with the web interface :

Problems related to Install :

Differentiation crashes :

Differentiated program doesn't compile :

Differentiated program crashes :

Returned Derivatives are wrong (or just need to be validated):

Functionalities :

Performance Improvements:

Documentation :

Acronym :

Include instructions accepted by Tapenade parsers:

Languages accepted by Tapenade parsers, Syntax Errors :

Syntax of directives that modify differentiation ($AD ...):

Language accepted by the A.D. engine ; Limitations:

Black-box procedures, unknown external or intrinsic procedures:

SPECIFYING BLACK-BOX ROUTINES IN *Lib FILES:

SPECIFYING BLACK-BOX ROUTINES WITH DUMMY ROUTINES:

Other Differentiation Modes:

Type mismatches:

Aliasing problems:

Missing differentiated routines for intrinsic or Black-Box routines:

ISIZE* constants all over the place:

Divisions by Zero and NaN's:

Domain of validity of derivatives:

Differences with Odyssée :

Documentation, Archives of the Mailing list :

Unsubscribe from the Mailing list

Want to cite Tapenade? :

PUSH/POP mechanism :

Original statements and results disappearing from the Reverse code :

Basic and extremely useful code preparation before differentiation

ALSO: CHECK THE SIZES OF PRIMITIVE TYPES:

THE FOLLOWING PREPARATION STEPS WERE USEFUL

FOR THE OLD VALIDATION METHOD ONLY

We keep them here for the record only, but they are not necessary!

Validation of the differentiated programs

VALIDATION AND DEBUGGING FOR TANGENT AD:

VALIDATION AND DEBUGGING FOR ADJOINT AD: (Assuming tangent AD is now correct !)

PROBLEMATIC INTERACTION WITH INDEPENDENT AND DEPENDENT PARAMETER SETS:

Independent and Dependent sets. Initialization and usage of the differentiated parameters

Question 1: What should the independent and dependent parameters be set as?

Question 2: What is the effect of a variable being in the independent and/or dependent sets, on the required initialization and returned value of its derivative?

Location of declaration and creation/allocation of differentiated scalars and arrays

Problems with web browsers (Macintosh):

Other AD tools:

Directory separator linux/windows:

JAVA errors: NullPointerException, ArrayOutOfBoundsException, etc:

Differentiating multiple top/head procedures, Differentiating Libraries:

Download Tapenade

Old versions of Tapenade

System errors of the "not found" sort:

System errors of the "out of memory" sort:

Sending remarks, questions, and bug reports:

JAVA Version required:

Wrong external's:

Placement of $AD directives:

Controlling checkpointing in the reverse mode ($AD NOCHECKPOINT):

Independent Iterations Loops ($AD II-LOOP):

Fixed-Point Loops ($AD FP-LOOP):

User-defined additional checkpoints ($AD CHECKPOINT-START and $AD CHECKPOINT-END):

User-defined fragments not-to-differentiate ($AD DO-NOT-DIFF and $AD END-DO-NOT-DIFF):

Binomial Checkpointing ($AD BINOMIAL-CKP):

Linear Solvers:

Multiple sessions in parallel:

Approximative source-code correspondence:

Too many Warning and Error messages:

Includes and Comments:

Default sizes of basic data types:

Parameterized array sizes:

Some cases of "segmentation fault":

Vector (i.e. Multi-directional) modes (i.e. option -multi or -vector):

Getting the Jacobian using the Multi-directional mode:

Second Derivatives and Hessians:

TANGENT-ON-TANGENT APPROACH:

TANGENT-ON-REVERSE APPROACH:

Differentiating MPI:

FIRST STEP: INSTALL AND SWITCH TO AMPI

SECOND STEP: DIFFERENTIATE

WARNING:

Syntax of directives that modify differentiation (`$AD ...`):

Placement of `$AD` directives:

Controlling checkpointing in the reverse mode (`$AD NOCHECKPOINT`):

Independent Iterations Loops (`$AD II-LOOP`):

Fixed-Point Loops (`$AD FP-LOOP`):

User-defined additional checkpoints (`$AD CHECKPOINT-START` and `$AD CHECKPOINT-END`):

User-defined fragments not-to-differentiate (`$AD DO-NOT-DIFF` and `$AD END-DO-NOT-DIFF`):

Binomial Checkpointing (`$AD BINOMIAL-CKP`):

Vector (i.e. Multi-directional) modes (i.e. option `-multi` or `-vector`):