What is Automatic Differentiation?¶
How can one obtain derivatives? 
Automatic Differentiation Computer Programs and Mathematical
Functions Activity of variables Focus on the directional derivatives
(tangents) Focus on the gradients Focus on multi-directional mode How can one obtain
derivatives? 
There are many ways to obtain derivatives. Maybe the most
straightforward is to go back to the equations that led to
the program. Suppose that some result is defined by some equations,
and the program solved these equations for this result. Then one
can write a new set of equations, whose solutions are the
derivative of the initial result. Consequently, one can write a new
program that solves these new equations for the desired
derivatives. This is mathematically very sound, but it probably is
the most expensive way, since it implies discretizing new
equations, then writing a new program. We all know how difficult
this is, and how many errors can be done! Moreover, in some cases
there are no simple original equations, and only the program is at
hand. Therefore we are looking for another way, more economical and
that uses only the original program.Using only the original program, one can naturally do divided differences. For a given set of program's inputs, X, the program P has computed a result P(X)=Y. In the general case, both X and Y are vectors, i.e. are composed of several real numbers. Given now some normalized direction dX in the space of the inputs, one can run the program P again, on the new set of inputs X+
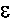dX, where 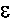is some very small positive number. Then
a good approximation of the derivative is computed easily
by: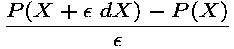
The centered divided differences, computed by:
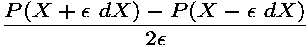
usually give a better approximation, but cost an additional execution of program P. Of course this is just an approximation of the derivatives. Ideally, the exact derivative is the limit of these formulas, when
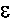tends to zero. But this makes no sense
on a real computer, since very small values of 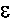lead to truncation errors, and therefore
to erroneous derivatives. This is the main drawback of divided
differences: some tradeoff must be found between truncation errors
and approximation errors. Finding the best 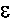requires numerous executions of the
program, and even then the computed derivatives are just
approximations. Automatic Differentiation
:
Automatic Differentiation, just like divided differences,
requires only the original program P. But instead of
executing P on different sets of inputs, it builds a
new, augmented, program P', that computes the
analytical derivatives along with the original program. This
new program is called the differentiated program. Precisely,
each time the original program holds some value v,
the differentiated program holds an additional value
dv, the differential of v.
Moreover, each time the original program performs some operation,
the differentiated program performs additional operations dealing
with the differential values. For example, if the original program,
at some time during execution, executes the following instruction
on variables a, b, c, and array
T:then the differentiated program must execute additional operations on the variables and their differentials da, db, dc, and array dT, that must somehow amount to:
The derivatives are now computed analytically, using the well known formulas on derivation of elementary operations. Approximation errors have just vanished.
Again, there are two ways to implement A.D.:
- Overloading consists in telling the compiler that each real number is replaced by a pair of real numbers, the second holding the differential. Each elementary operation on real numbers is overloaded, i.e. internally replaced by a new one, working on pairs of reals, that computes the value and its differential. The advantage is that the original program is virtually unchanged, since everything is done at compile time. The drawback is that the resulting program runs slowly because it constantly builds and destroys pairs of real numbers. Moreover, it is very hard to implement the "reverse mode" with overloading.
- Source transformation consists in adding into the program the new variables, arrays, and data structures that will hold the derivatives, and in adding the new instructions that compute these derivatives. The advantage is that the resulting program can be compiled into an efficient code, and the "reverse mode" is possible. The drawback is that this is an enormous transformation, that cannot be done by hand on large programs. Tools are needed to perform this transformation correctly and rapidly. Our team studies this sort of tools. Our Tapenade engine is just one such Automatic Differentiation tool that uses source transformation.
- One may really want the derivative of the program. More
exactly, since the program's inputs and outputs are generally
vectors, the derivative is a matrix, known as the
Jacobian matrix, Each element (i,j) of the
Jacobian matrix is the partial derivative
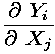
of output Yi with respect to input Xj. For that, the derivative object that must be computed along with each value v is the vector of all partial derivatives of v with respect to each input. When values are themselves arrays, the derivative object becomes a matrix. This leads to carrying partial Jacobian matrices along with the main computation stream. This is usually expensive in time and memory space. This drawback can be partially coped for, using sparse representations for the derivative objects. - One may simply want directional derivatives, also known as tangents. This means that, instead of the explicit Jacobian matrix J, one just needs its effect on a given direction vector dX in the input space. This effect is actually dY = J * dX, but one can evaluate it without explicitly computing J. For that, the derivative object that must be computed along with each value v is its "differential" dv, i.e. (the first-order approximation of) the quantity by which v varies when the input X varies by dX. As expected, this is far less expensive than building the whole Jacobian. Note that directional derivatives also can provide us with the Jacobian matrix, if directional deriatives are computed for each canonical direction in the input space. In other words, this requires one computation of the directional derivative per input variable, and even less than that, if one knows that the Jacobian matrix is sufficiently sparse.
- One may want gradients. When there is only one output, the Jacobian matrix has only one line, which is exactly the gradient of the result with respect to the inputs. When there are many outputs, one defines a scalar composite result, i.e. some linear combination of these outputs, so as to compute the gradient of this result. To put it differently, one wants a combination of the lines of the Jacobian Xb* = Yb* * J. The "*" superscript indicates transposition, i.e. Xb* and Yb* are row vectors. This can be computed without explicitly computing J. For that, the derivative object is called an "adjoint", and it is computed in the reverse of the original program's order, and will be shown later. Like with the directional derivatives, one can compute the whole Jacobian matrix by repeatedly computing gradients, for each canonical direction in the output space, or fewer than that when the Jacobian is sparse. It is easy to check that this approach is advisable when there are far more inputs than outputs.
- One may want higher-order derivatives (Hessian). This can be done computing a derivative object which is a partial Hessian tensor. Since this might be very expensive, another approach is to compute directional higher-order derivatives, and use them afterwards to recompute the coefficients of the Hessian. (cf [GriewankUtkeWalther97])
- One may want directional higher-order derivatives. Given a direction vector dX in the input space, one computes along the original program a derivative object that contains the first and higher derivatives of each intermediate value in the direction dX. Higher-order derivatives are useful to get a more accurate approximation, or to optimize more efficiently.
- One may want Taylor series expansions. (cf [Griewank00])
- One may want to compute intervals. This is not strictly speaking a matter of derivatives, but shares many similarities. The derivative object computed along with each value v is the interval into which this value may range.
Computer Programs and
Mathematical Functions :
Before we can focus on directional derivatives and
gradients, we need to introduce a general framework in which
we can describe precisely these two modes of A.D. Essentially, we
identify programs with sequences of instructions,
themselves identified with composed functions.Programs contain control, which is essentially discrete and therefore non-differentiable. We identify a program with the set of all possible run-time sequences of instructions. Of course there are many such sequences, and therefore we never build them explicitly. The control is just how one tells the running program to switch to one sequence or another. For example this small program piece:
if (x <= 1.0) then
printf("x too small\n");
else {
y = 1.0;
while (y <= 10.0) {
y = y*x;
x = x+0.5;
}
}printf("x too small\n");
y = 1.0;
y = 1.0; y = y*x; x = x+0.5;
y = 1.0; y = y*x; x = x+0.5; y = y*x; x = x+0.5;
y = 1.0; y = y*x; x = x+0.5; y = y*x; x = x+0.5; y = y*x; x = x+0.5;and so on...
Each of these sequences is "differentiable". The new program generated by Automatic Differentiation contains of course some control, such that each of its run-time sequences of instructions computes the derivative of the corresponding sequence of instructions in the initial program. Thus, this differentiated program will probably look like (no matter whether by overloading or by source transformation):
if (x <= 1.0) then
printf("x too small\n");
else {
y = 1.0;
dy = 0.0;
while (y <= 10.0) {
dy = dy*x + y*dx;
y = y*x;
x = x+0.5;
}
}Now that programs are identified with sequences of instructions, these sequences are identified with composed functions. Precisely, the sequence of instructions :
is identified to the function :
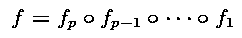
Of course each of these functions are extended to operate on the domain of all the program variables, but variables not overwritten by the instruction are just transmitted unchanged to the function's result. We can then use the chain rule to formally write the derivative of the program for a given vector input x :
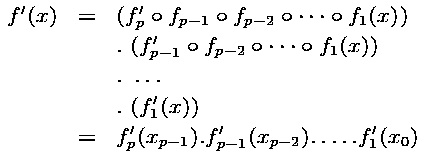
We wrote f'n for the derivatives of function fn. The f'n are thus Jacobian matrices. To write the above in a shorter form, we introduced xn, which is the values of the variables just after executing the first n functions (we set x0 = x).
Therefore, computing the derivatives is just computing and multiplying these elementary Jacobian matrices f'n(xn-1)
Activity of variables :
In practice, not all the elements of the Jacobian matrix need to be
computed. Some elements can be proved to be always null, some
others are simply not needed by the end user. We can take this into
account to simplify the differentiated program. This is summarized
by the notion of activity of an instance of a variable. The
end-user specifies a set of output variables, for which the
derivatives are requested. These are called the dependent
variables. The end-user also specifies a set of input variables,
with respect to which the dependent output must be
differentiated. These are called the independent variables.
We shall say that an instance of a variable is active if
- it depends on some independent, in a differentiable way, and
- some dependent depends on it, in a differentiable way.
Focus on the directional
derivatives (tangents):
Computing the product of all the elementary Jacobian matrices
returns the complete Jacobian matrix J of f.
This is certainly expensive in time and space. Often, one just
wants a directional derivative dY = J * dX. If we
replace J = f'(x) by its above expansion with the
chain rule, we obtain :
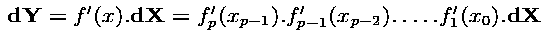
which must be computed from right to left, because "matrix time vector" products are so much cheaper than "matrix times matrix" products. Things are easy here, because x0 is required first, then x1, and so on. Therefore differentiated instructions, that compute the Jacobian matrices and multiply them, can be done along with the initial program. We only need to interleave the original instructions and the derivative instructions. This is called the tangent mode of Automatic Differentiation.
In the tangent mode, the differentiated program is just a copy of the given program, Additional derivative instructions are inserted just before each instruction that involves active variables. Each active variable gives birth to a new variable, of same type and size, which is called its derivative variable. The control structures of the program are unchanged, i.e. the Call Graph and Flow Graph keep the same shape.
Here is an example. Consider the original (piece of) program:
... v2 = 2*sin(v1) + 5 if (v2>0.0) then v4 = v2 + p1*v3/v2 p1 = p1 + 0.5 endif call sub1(v2,v4,p1) ...
... dv2 = 2*cos(v1)*dv1 v2 = 2*sin(v1) + 5 if (v2>0.0) then dv4 = dv2*(1-p1*v3/(v2*v2)) + dv3*p1/v2 v4 = v2 + p1*v3/v2 p1 = p1 + 0.5 endif call sub1_d(v2,dv2,v4,dv4,p1) ...
Intrinsic functions, such as sin, are differentiated directly, "in line", using an external configuration file which specifies, for example, that the (partial) derivative of sin(x) with respect to x is cos(x)
The structure of subroutine calls is also preserved, but differs slightly: Since a routine call is in fact a shorthand for another piece of program, and that this piece of program will be augmented with differentiated instructions too, the call to the differentiated routine sub1_d simply replaces the call to sub1. In other words sub1_d does the previous work of sub1 plus the derivatives computations. Of course, these derivative instructions use the derivative variables, and therefore each parameter which is active at the beginning or at the end of the routine requires an extra parameter holding its derivative.
Consider now the special case of a call to a black-box routine. This is basically the same as the FORTRAN EXTERNAL routines but we generalize it as follows: we call black-box a routine on which we cannot, or must not, or do not want to run AD! This can be because we don't have the source for it (EXTERNAL routines), or because we want to provide a much better hand-written derivative routine. In this case, AD of the calling program needs additional information about the black-box routine. Suppose that sub1 above is black-box. If AD knows nothing about it, then it must make the conservative assumption that p1, although not active at call time, may become active at return time. For example, its exit value might depend on the active input v2. Therefore AD must introduce a derivative dp1, initialized to 0.0 before the call, and containing some nontrivial result upon return. The last lines of the differentiated code should be:
... dp1 = 0.0 call sub1_d(v2,dv2,v4,dv4,p1,dp1) ...
This matrix can capture precise behavior. For example it also implies here that although the entry active v2 is used to compute the exit, active, v4, the exit v2 is not active any more, because it only depends on the input p1, which is not active. When AD is provided with this dependence matrix for black-box sub1 (e.g. in an external configuration file), it generates a program that calls
call sub1_d(v2,dv2,v4,dv4,p1)
+ non-specialization principle for multiple routine calls + specifics of commons, data structures non-specialization principle.
This is all we will say here about the general principles of AD in direct mode. To go further, you may read the Tapenade reference article and the Tapenade 2.1 users guide, that will describe conventions about variable names and declarations, differentiation of individual instructions and control structures, and in general all you must know to understand and use differentiated programs produced by Tapenade.
Focus
on the gradients :
Whereas the tangent mode of AD is maybe the
most immediate, it turns out that many applications indeed need
gradients. The reverse mode of AD does just that! In fact,
the reverse mode computes gradients in an extremenly efficient way,
at least theoretically. This is why it is one of the most promising
modes of AD.Strictly speaking, the gradient of a function f is defined only when f returns a scalar. In other words, there can be only one optimization criterion. If f returns a vector Y of results, we must define from Y a scalar composite result, i.e. a linear combination of its elements. We write this scalar optimization criterion as a dot product
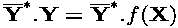
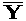is
nothing but the vector of the weights of each component of
Y. The gradient of this scalar optimization criterion is
therefore, after transposition:
Again, this is most efficiently computed from right to left, because matrix-times-vector products are so much cheaper than matrix-times-matrix products. This is the principle of the reverse mode.
This turns out to make a very efficient program, at least theoretically (cf Section 3.4 of [Griewank00]). The computation time required for the gradient is only a small multiple of the run time of the original program. It is independent from the number of inputs in X. Moreover, if there are only a small number m of scalar outputs in Y, one can compute the whole Jacobian matrix row by row very efficiently.
However, we observe that the Xn are required in the inverse of their computation order. If the original program overwrites a part of Xn, the differentiated program must restore it before it is used by f'n+1(Xn).
- Recompute All (RA): the
Xn is recomputed when needed, restarting
the program on input X0 until instruction
In. The TAF tool uses this strategy. The
following figure illustrates the RA strategy:
- Store All (SA): the
Xn are restored from a stack when needed.
This stack is filled during a preliminary run of the program, the
"forward sweep", that additionally stores variables on the
stack just before they are overwritten. The tools Adifor and
Tapenade use this strategy. The following figure illustrates the
SA strategy:
- In Recompute All (RA) mode, the
result of checkpointing part P is shown on the top of next
figure. The snapshot (big black dot) memorizes the state of
the program just after P.
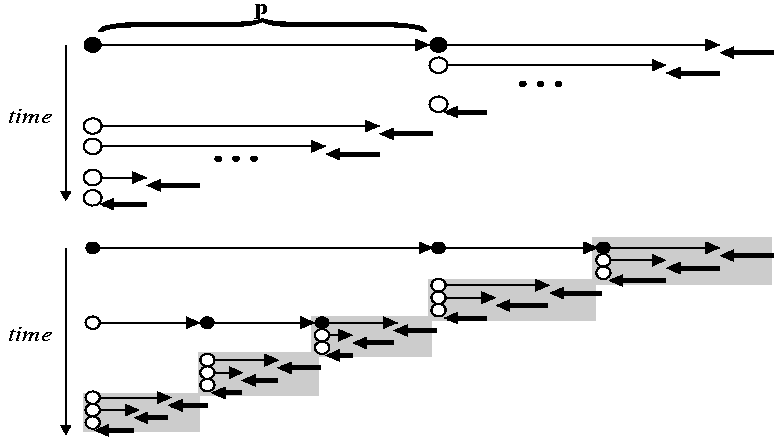
- In Store All (SA) mode, the result
of checkpointing part P is shown on the top of next figure.
The snapshot (big black dot) memorizes the state of the
program just before P. There is an additional cost, which is
the duplicate execution of P.
In the sequel, we shall concentrate on the Store All (SA) strategy.
The structure of a reverse differentiated program is therefore more complex than in the tangent mode. There is first a forward sweep, identical to the original program augmented with instructions that memorize the intermediate values before they are overwritten, and instructions that memorize the control flow in order to reproduce the control flow in reverse during the backward sweep. Then starts the backward sweep, that actually computes the derivatives, and uses the memorized values both to compute the derivatives of each instruction and to choose its flow of control. Here is the same example as for the tangent mode. Consider again this original (piece of) program:
... v2 = 2*sin(v1) + 5 if (v2>0.0) then v4 = v2 + p1*v3/v2 p1 = p1 + 0.5 endif call sub1(v2,v4,p1) ...
... push(v2) v2 = 2*sin(v1) + 5 if (v2>0.0) then push(v4) v4 = v2 + p1*v3/v2 push(p1) p1 = p1 + 0.5 push(true) else push(false) endif push(v2) push(v4) push(p1) call sub1(v2,v4,p1) ...
... pop(p1) pop(v4) pop(v2) call sub1_b(v2,v2b,v4,v4b,p1) pop(control) if (control) then pop(p1) pop(v4) v3b = v3b + v4b*p1/v2 v2b = v2b + v4b*(1-p1*v3/(v2*v2)) v4b = 0.0 endif pop(v2) v1b = v1b + v2b*2*cos(v1) v2b = 0.0 ...
The additional parameters passed to the call to sub1_b strongly depend on the results of activity analysis. If an argument is not active at the entry into the procedure nor at the exit from the procedure, then we need not pass a derivative argument. Otherwise we must pass one, and it must be initialized when necessary.
When the procedure is a function, then its derivative procedure may have an extra derivative parameter, which is the differential of the function's output. On the other hand, the function's output itself can very well be forgotten: remember the call to the derivative function are enclosed in a backward sweep, so there is no one left there to use this function's result!
This is all we will say here about the general principles of AD in reverse mode. To go further, you may read the Tapenade reference article and the Tapenade 2.1 user's guide, that will describe conventions about variable names and declarations, differentiation of individual instructions, control structures, procedure calls, and in general all you must know to understand and use differentiated programs produced by Tapenade.
Focus
on multi-directional mode :
...